A barra uniforme esbelta de é articulada em relação a um eixo horizontal através de e liberada a partir do repouso na posição horizontal. Determine a distância do centro de massa até que resultará em uma aceleração angular inicial de , e encontre a força na barra em imediatamente após a liberação.
Passo 1
Vamos começar com um esquema da situação:
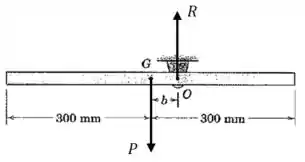
O momento de inércia em relação ao ponto pode ser calculado usando o teorema dos eixos paralelos:
Passo 2
Agora vamos analisar a soma dos momentos em relação ao ponto , sabendo que a acelereração angular observada é .
E podemos resolver essa equação do segundo grau para encontrar :
E as duas soluções são ou . Como a primeira solução é quase do tamanho da própria barra (o que não bate com a representação do desenho), ficamos apenas com a segunda:
Passo 3
Falta encontrar a força em . Para isso vamos usar a segunda lei de Newton.
Já que a barra se move com aceleração angular em torno do ponto , então (imediatamente após a liberaçao da barra) o centro de massa se move para baixo com a seguinte aceleração tangencial:
Então:
Resposta
e .