Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 40
Se o momento de atrito no mancal é de , determine a aceleração angular do tambor ranhurado, que possui uma massa de e um raio de giração .
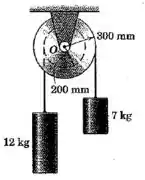
Passo 1
Vamos começar com um esquema da situação:
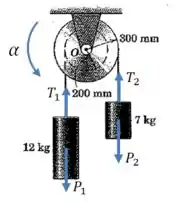
Ok, então nós temos três incógnitas nesse problema, as trações e nas cordas, e a aceleração angular do tambor.
Isso quer dizer que vamos precisar montar três equações para resolver o problema.
Passo 2
Vamos começar com as equações das forças que agem sobre cada cilindro. Em cada caso, a aceleração do cilindro será a aceleração angular do tambor multiplicada pelo raio do círculo onde cada corda está enrolada no tambor.
Começando pelo cilindro de :
E o peso deve aparecer com um sinal negativo, já que ele é contrário à aceleração angular que definimos:
E fazendo a mesma coisa para o cilindro da esquerda, encontramos o seguinte:
E agora temos que inverter os sinais da tração e do peso:
Passo 3
E a nossa terceira equação virá dos momentos que agem no tambor. Além dos momentos gerados pelas trações e , temos o momento de atrito de , que se opõe à rotação:
E então ficamos com um sistema de três equações:
Vamos substituir os valores:
Vamos multiplicar a segunda equação por , e a terceira por , e então somar todas:
Resposta
A aceleração angular é .