Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 51
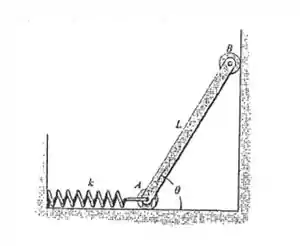
A barra uniforme tem um peso . Determine o ângulo para o equilíbrio. A mola está livre quando . Despreze o peso dos roletes.
Passo 1
Como o enunciado foi bem direto com relação ao que ele queria, vamos partir direto para a resolução. Como o centro de gravidade está acima do nosso ponto de partida que no caso é o ponto , sua energia potencial é positiva. Aqui vamos ter e a mola comprime . Dessa forma, vamos ter
O equilíbrio ocorre quando Sendo, assim, vamos derivar em relação ao ângulo
Resposta
Exercícios de Livros Relacionados
42- A figura mostra a seção transversal de um basculante de ventilação de 60k g , articulado em O ao longo de sua borda horizontal superior. O basculante é controlado pelo cabo acionado por uma mola,
46- A alavanca está presa a uma das engrenagens montadas sobre mancais fixos, que estão ligadas por uma mola. A mola de rigidez k liga dois pinos, montados nas faces das engrenagens. Quando a alavanca
47- A seção transversal de um basculante articulado em relação ao eixo horizontal O , de massa m e com centro de massa em G , está mostrada na figura. A medida que o basculante abre, a mola é comprimi
48- Determine a altura máxima h da massa m para a qual o pêndulo invertido será estável na posição vertical mostrada. Cada uma das molas tem rigidez k e elas estão igualmente pré-comprimidas nessa pos
49- U m pequeno elevador industrial, acionado a pedal, está mostrado na figura. Existem quatro molas idênticas, duas de cada lado do eixo central. A rigidez de cada par de molas vale 2 k . Ao projetar