Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 42

42- A figura mostra a seção transversal de um basculante de ventilação de 60   k g , articulado em O ao longo de sua borda horizontal superior. O basculante é controlado pelo cabo acionado por uma mola, que passa sobre a pequena polia em A . A mola tem uma rigidez de 160   N por metro de alongamento e está sem deformação quando θ = 0 . Determine o ângulo θ para haver equilíbrio.

Passo 1

Desenhando as medidas pertinentes conseguimos descobrir a energia potencial gravitacional desse sistema.

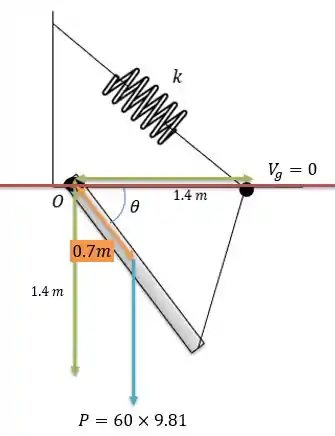
Pela base do sistema ser a reta O A temos que o centro de massa da barra encontra-se abaixo do eixo nulo de energia potencial gravitacional (tendo sinal negativo), logo se espelharmos a reta laranja na vertical nós iremos ter uma energia potencial gravitacional igual a:

V g = m g h = - 60 × 9.81 × 0.7 sin ⁡ θ = - 412.02 sin ⁡ θ

Passo 2

Agora para encontrar a energia potencial elástica devemos traçar conhecer a geometria do sistema.

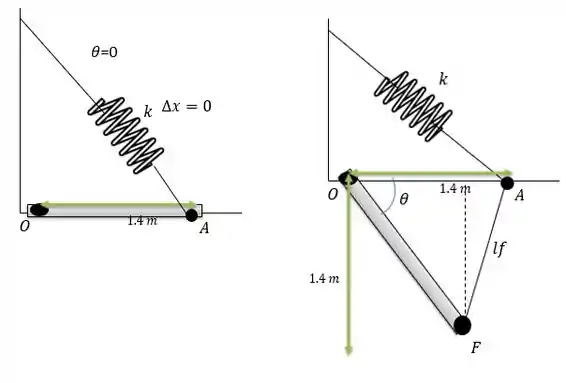
Quando θ = 0 a barra encontra-se totalmente na horizontal e quando a barra gira em sentido de θ o lado F A fica com um tamanho l f essa variação de tamanho faz esticar a mola de modo que ela agora tenha a tamanho igual a:

Δ x = l f

Para calcular l f vamos destacar o triângulo e trabalhar ele um pouco melhor:

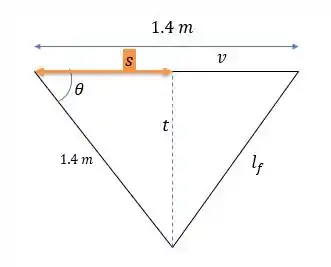
Calculando o cosseno do ângulo θ nós temos:

cos ⁡ θ = s 1.4 → s = 1.4 cos ⁡ θ

E o seno:

sin ⁡ θ = t 1.4 → t = 1.4 sin ⁡ θ

Logo o valor de v será:

s + v = 1.4 → v = 1.4 - 1.4 cos ⁡ θ = 1.4 ( 1 - cos ⁡ θ )

Fazendo Pitágoras agora no triângulo retângulo direito nós temos:

l f 2 = v 2 + t 2

l f 2 = 1.4 2 ( 1 - cos ⁡ θ ) 2 + 1.4 2 sin 2 ⁡ θ

l f 2 = 1.4 2 [ 1 - 2 cos ⁡ θ + cos 2 ⁡ θ + sin 2 ⁡ θ ] = 2 × 1.4 2 [ 1 - c o s θ ]

Logo a energia potencial elástica do sistema é:

V e = 1 2 K l f 2

Para K = 160 temos:

V e = 160 × 1.4 2 [ 1 - cos ⁡ θ ]

Então a energia total do sistema será:

V = 160 × 1.4 2 [ 1 - cos ⁡ θ ] - 412.02 sin ⁡ θ

Passo 3

Derivando em relação a θ a equação da energia nós temos:

d V d θ = 160 × 1.4 2 sin ⁡ θ - 412.02 cos ⁡ θ

Igualando a equação a zero nós encontramos o equilíbrio do sistema:

160 × 1.4 2 sin ⁡ θ - 412.02 cos ⁡ θ = 0

160 × 1.4 2 sin ⁡ θ = 412.02 cos ⁡ θ

Dividindo os dois lados por cosseno nós teremos:

160 × 1.4 2 t g   θ = 412.02

t g θ = 412.02 160 × 1.4 2

Fazendo a tangente desse valor nós encontramos:

θ = 52.72 °

Resposta

θ = 52.72 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a altura h do bloco B de modo que a barra esteja sempre em equilíbrio. As molas estão livres quando a barra está na posição vertical. O bloco tem um peso W .
Um furo cônico é perfurado no fundo do cilindro, e depois é apoiado na barra em A . Determine a distância mínima d a fim de que ele permaneça em equilíbrio estável.
A mola conectada ao mecanismo tem um comprimento livre quando θ = 90 ° . Determine a posição θ para o equilíbrio e investigue a estabilidade do mecanismo nessa situação. O disco A é conectado por pino
Determine a força P que deve ser aplicada à corda enrolada no tambor em C necessária para levantar o balde tendo uma massa m . Observe que, enquanto o balde é levantado, a polia enrola uma corda no ei
A barra uniforme A B pesa 500 N . Se as duas molas D EeB C estão livres quando θ = 90 ° , determine o ângulo θ para equilíbrio usando o princípio da energia potencial. Investigue a estabilidade na pos