Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 109
Uma barra uniforme tendo uma massa de kg é suportada por um pino em de um rolete que corre sobre um trilho horizontal. Se a barra está originalmente em repouso, e uma força horizontal é aplicada ao rolete, determine a aceleração do rolete. E suponha que o rolete em A é substituído por um bloco deslizante. O coeficiente de atrito cinético entre o bloco o trilho é . Despreze a massa do rolete e sua dimensão nos cálculos e a dimensão e massa do bloco.
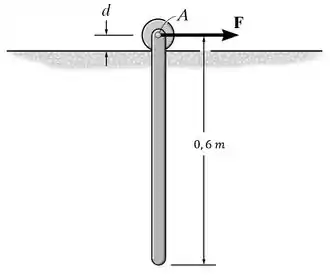
Passo 1
Os diagramas de corpo livre e cinemático do problema em análise são mostrados na figura abaixo:
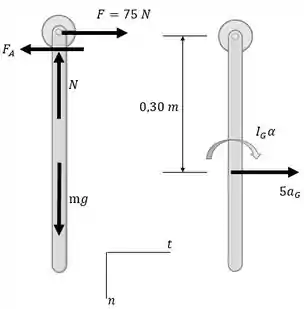
O momento de inércia de massa para uma haste com a massa concertada no centro pode ser calculado por,
Passo 2
Tendo as informações do DCL e do DC, é possível aplicar 2º lei de Newton para a análise do corpo. Note que no intante em que a força é aplicada, a velocidade angular da haste é nula . Portanto a aceleração normal do centro de massa da haste é nula .
Passo 3
No rolete a velocidade angular é nula e . A aceleração do rolete A pode ser obtido a partir da análise da aceleração relativa entre o ponto A e o centro de massa G.
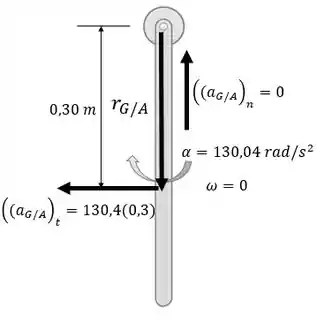
Resposta
A força normal do rolete é N, a aceleração angular é rad/s2 a aceleração do rolete é m/s2