Determine a coordenada do centroide do corpo mostrado na figura. (Dica: use o resultado do Problema Resolvido 5.13.)
Passo 1
Bom galera, o problema quer que a gente encontre o centroide do corpo da figura, que a gente pode simplificar bem assim:

A fórmula básica para encontrar o centroide é:
Passo 2
Show de bola, nós então montamos uma tabelinha simples com os volumes e os de cada solido que a gente conseguir separar pra facilitar, esse a gente encontrar lá no final do livro, então bora:
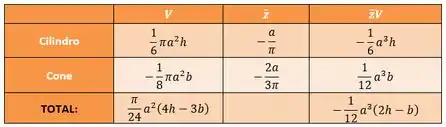
Passo 3
Por fim, a gente aplica aquela formula básica: