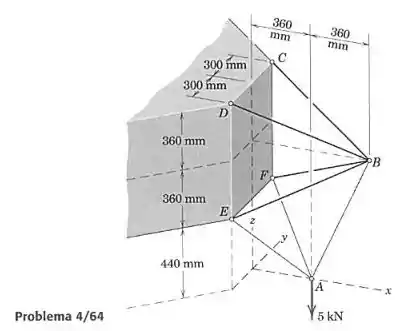
A seção da treliça piramidal é simétrica em relação ao plano vertical como mostrado. Os cabos , e suportam uma carga de 5 kN. Determine a força no elemento .
Passo 1
Vamos calcular as forças pelo método dos nós. Primeiro colocamos a força na forma de módulo vezes vetor unitário, e depois fazemos a equação de equilíbrio para o nó, nas três direções. Para o nó só temos 3 incógnitas, então conseguimos resolver as equações, encontrando e . Depois vamos para o nó e determinamos .
Passo 2
Vamos fazer as equações para o nó . Representamos , e em vetores unitários. Primeiro :
Agora para :
Pela simetria, é a mesma coisa que , mas com a componente ao contrário:
Passo 3
Agora que temos as forças, somamos todas e igualamos a zero. Não podemos esquecer da carga igual a .
Agrupando os termos em cada direção:
Pela simetria, sabemos que . Então:
Da direção , tiramos:
Da direção :
Substituindo :
Não precisamos dos valores de e de , pois não aparecem para o nó .
Passo 4
Vamos agora às equações para o nó . Primeiro vamos fazer algumas considerações que vão facilitar muito nas contas. Pela simetria, vamos ter:
Pela configuração geométrica simétrica das barras, sabemos também que os vetores unitários de , , e são iguais, só mudando os sinais das direções. Vamos calcular então o vetor unitário só para uma delas. Escolhemos :
Com isso os outros vetores unitáros ficam definidos, trocando os sinais:
Além disso, vamos colocar em função de e em função de :
Passo 5
Agora só temos 2 incógnitas, e . Vamos somar todas as forças de e igualar a zero:
Substituindo o módulo de igual a 3,55 kN:
Primeiro para a direção , temos:
Dividindo tudo por 1,68:
Agora para a direção :
Dividindo tudo por 0,838 e substituindo :