Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 18

Um bastão de vidro uniforme, com comprimento L , é colocado na vasilha hemisférica lisa com raio r . Determine o ângulo de inclinação θ para que haja equilíbrio.

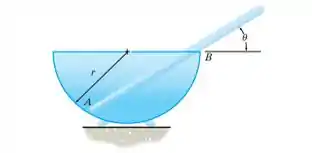
Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Não se assustem com a geometria da questão e com o que ele nos pede! Vamos fazer devagar que vai dar tudo certo!

Queremos determinar um ângulo θ para que haja equilíbrio. Então, se estamos falando de equilíbrio, lembramos que:

∑ F = 0 ∑ M = 0

Nosso objetivo aqui é obter equações para determinar o θ que satisfaz as relações acima!

Mas como iremos obter estas equações? Bom, para isto precisamos do diagrama de forças do nosso problema! Fazendo um esboço, temos:

Agora que marcamos todas as forças (duas normais apenas e uma força peso) e seu ponto de atuação, vamos as contas!

Passo 2

Nosso trabalho agora é aplicar as equações de equilíbrio para o esboço feito no Passo 1. O sistema de coordenadas foi escolhido de forma que o eixo x é colinear com a haste, algo que facilitará muito nos cálculos.

Então, escolhendo o ponto B para analisarmos (assim eliminará a força N 2 no cálculo do momento), temos:

∑ F x = 0 ∑ F y = 0 ∑ M B = 0 ⟹ N 1 cos ⁡ θ - P cos ⁡ 90 ° - θ = 0 N 1 sen ⁡ θ + N 2 - P sen ⁡ 90 ° - θ = 0 P sen ⁡ 90 ° - θ a - N 1 sen ⁡ θ L 2 + a = 0

N 1 cos ⁡ θ - P sen ⁡ θ = 0 N 1 sen ⁡ θ + N 2 - P cos ⁡ θ = 0 P cos ⁡ θ a - N 1 sen ⁡ θ L 2 + a = 0

Só que não conseguimos resolver o sistema acima, pois temos quatro incógnitas N 1 , N 2 , θ , a e apenas três equações. Precisamos de uma quarta equação para que possamos resolver o nosso sistema!

E esta quarta equação vem exatamente da geometria do problema. Nele nós temos:

cos ⁡ θ = L 2 + a 2 r ⟹ cos ⁡ θ = L 2 + a 2 r ⟹ L 2 + a = 2 r cos ⁡ θ

a = 2 r cos ⁡ θ - L 2

E assim chegamos ao seguinte sistema:

N 1 cos ⁡ θ - P sen ⁡ θ = 0 N 1 sen ⁡ θ + N 2 - P cos ⁡ θ = 0 P cos ⁡ θ a - N 1 sen ⁡ θ L 2 + a = 0 a = 2 r cos ⁡ θ - L 2

Passo 3

Nosso trabalho agora é resolver o sistema do final do Passo 2. Como nosso objetivo não é descobrir a força N 2 , nós não iremos trabalhar com a segunda equação do sistema, pois nela aparece a força N 2 .

Portanto, isolando a força P na primeira equação, temos:

N 1 cos ⁡ θ - P sen ⁡ θ = 0

P = N 1 cos ⁡ θ sen ⁡ θ

Substituindo esta relação e a equação 4 na terceira equação, temos:

P cos ⁡ θ a - N 1 sen ⁡ θ L 2 + a = 0

N 1 cos ⁡ θ sen ⁡ θ cos ⁡ θ 2 r cos ⁡ θ - L 2 - N 1 sen ⁡ θ L 2 + 2 r cos ⁡ θ - L 2 = 0

cos 2 ⁡ θ sen ⁡ θ 2 r cos ⁡ θ - L 2 - sen ⁡ θ 2 r cos ⁡ θ = 0

cos ⁡ θ sen ⁡ θ 2 r cos ⁡ θ - L 2 - 2 r sen ⁡ θ = 0

cos ⁡ θ 2 r cos ⁡ θ - L 2 - 2 r sen 2 ⁡ θ sen ⁡ θ = 0

2 r cos 2 ⁡ θ - L 2 cos ⁡ θ - 2 r sen 2 ⁡ θ = 0

Só que nós sabemos que cos 2 ⁡ θ + sen 2 ⁡ θ = 1 . Portanto,

2 r cos 2 ⁡ θ - L 2 cos ⁡ θ - 2 r 1 - cos 2 ⁡ θ = 0

4 r cos 2 ⁡ θ - L 2 cos ⁡ θ - 2 r = 0

cos 2 ⁡ θ - L 8 r cos ⁡ θ - 1 2 = 0

Resolvendo a equação do segundo grau acima (basta considerar a função cos ⁡ θ como uma incógnita x ) e obtendo o valor positivo (pois θ < 90 ° pela geometria do problema), temos:

cos ⁡ θ = L 2 + L 2 4 + 32 r 2 8 r ⟹ cos ⁡ θ = L + L 2 + 128 r 2 16 r

E assim chegamos à solução que buscamos:

θ = arccos ⁡ L + L 2 + 128 r 2 16 r

E assim finalizamos a questão!

Resposta

θ = arccos ⁡ L + L 2 + 128 r 2 16 r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três cabos estão unidos no anel de junção C . Determine as forças trativas nos cabos A C e B C causadas pelo peso do cilindro de 30k g .
Uma força axial de 700N é necessária para remover a polia de seu eixo. Que força F deve ser exercida nos cabos dos dois pés-de-cabra? O atrito nos pontos de contato B e E é suficiente para impedir des
Uma pessoa segura uma mala de 30k g pela alça como indicado na figura. Determine a força trativa em cada uma das quatro argolas idênticas A B .
Para facilitar a mudança de posição de um gancho para levantar carga quando ele está descarregado, usa-se o suporte deslizante mostrado. Os ressaltos em A e B se prendem aos flanges de uma viga caixão
Em um procedimento para avaliar a resistência do músculo tríceps, uma pessoa força para baixo uma célula de carga com a palma da mão, como mostrado na figura. Se a leitura da célula de carga é de 160N