Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 16
Uma força axial de é necessária para remover a polia de seu eixo. Que força deve ser exercida nos cabos dos dois pés-de-cabra? O atrito nos pontos de contato e é suficiente para impedir deslizamento; o atrito nos pontos de contato e com a polia é desprezível.
Passo 1
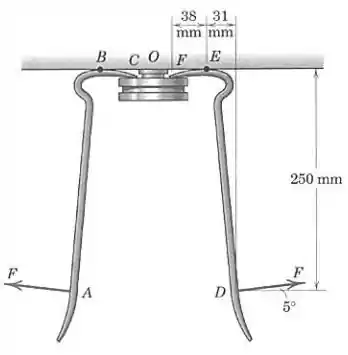
Como há simetria entre os lados direito e esquerdo, vamos analisar só o lado direito do sistema. Note que, no ponto do pé-de-cabra, deve atuar uma força para cima cujo módulo é metade de (simetria), pois é a reação da força com que o pé-de-cabra empurra a polia para baixo.
Vamos chamar essa força de , e será seu momento em torno de :
Passo 2
A força pode ser decomposta em suas componentes horizontal e vertical, de modo que o momento em torno de causado por essa força deve ser a soma dos momentos de cada componente:
Passo 3
Como não há rotação, o momento total em torno de deve ser nulo: