Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 5
Um bloco de 32 kg é ligado a uma mola e pode mover-se sem atrito em um rasgo como mostrado na figura. O bloco está na sua posição de equilíbrio quando é atingido por um martelo que lhe confere uma velocidade inicial de 250 mm/s. Determine (a) o período e a frequência do movimento resultante, (b) a amplitude do movimento e a aceleração máxima do bloco.
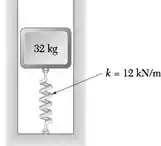
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente encontre o período e a frequência do movimento resultante, (b) a amplitude do movimento e a aceleração máxima do bloco.
Então vem comigo começando pela frequência utilizando a equação da posição :D
-
Passo 2
- Em
Considerando
Resposta
Exercícios de Livros Relacionados
O cilindro hidráulico B C do caminhão basculante está quebrado e desconectado. O motorista (que fez curso de dinâmica) decide calcular a aceleração mínima a do caminhão necessária para inclinar o depó
Uma bola de boliche de 6,4k g com uma circunferência de 690m m tem um raio de giração de 83m m . Se a bola é lançada com uma velocidade de 6m / s , mas sem velocidade angular quando toca o chão da pis
A porta de garagem suspensa é um painel retangular homogêneo de massa m e é guiada por seus roletes nas extremidades, que correm nos trilhos mostrados (tracejados). Se a porta é liberada a partir do r
O caminhão transporta uma bobina com 1500m m de diâmetro de um cabo com massa de 0,75k g por metro de comprimento. Existem 150 voltas na bobina cheia. A bobina vazia possui uma massa de 140k g , com r
Os pequenos roletes nas extremidades da barra esbelta uniforme de 3,6k g estão limitados a se deslocar nas ranhuras que se situam em um plano vertical. No instante em que θ = 30 ° , a velocidade angul