Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 106
Uma bola de boliche de com uma circunferência de tem um raio de giração de . Se a bola é lançada com uma velocidade de , mas sem velocidade angular quando toca o chão da pista, calcule a distância percorrida pela bola antes que comece a rolar sem deslizar. O coeficiente de atrito entre a bola e o piso é de .
Passo 1
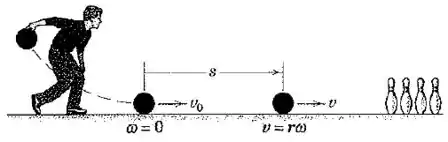
A bola começa o movimento com uma velocidade que é alta demais para que a bola role sem deslizar.
Conforme ela percorre a pista, que tem certo coeficiente de atrito, a sua velociadde vai ser reduzida até um valor em que ela começa a rolar sem deslizamento.
Nesse ponto, pela primeira vez desde o início do movimento, a velocidade do centro de massa vai obedecer à seguinte relação:
Então imagine o seguinte: depois que a bola é lançada, a sua velocidade angular começa a aumentar, e a sua velocidade do centro de massa começa a diminuir. Quando as duas são “iguais”, aí temos rolamento sem deslizamento.
Obs.: “Iguais” no sentido de que são proporcionais uma a outra, tendo o raio da bola como constante de proporcionalidade.
Passo 2
Vamos começar olhando para os tempos que cada grandeza leva para chegar até o ponto que queremos.
Depois de lançada, a única força horizontal agindo sobre a bola será a força de atrito (no sentido que se opõe ao movimento), então a segunda lei de Newton diz que a aceleração da bola será a seguinte:
Quando está sujeita a essa aceleração, quanto tempo a bola leva para ser desacelerada de até uma velocidade ?
Ok, esse é o tempo que a velocidade do centro de massa demora para diminuir até o valor que precisamos.
Passo 3
Agora vamos pensar na velocidade angular. A força de atrito realiza um momento em relação ao centro de massa da bola e, portanto, produz uma aceleração angular:
E o momento de inércia da bola em relação a um eixo que passa pelo seu centro de massa pode ser calculado usando o seu raio de giração :
E como a bola tem velocidade angular inicial , o tempo que demora para atingir o valor que queremos é:
Lembrando que o valor que queremos é , então:
Esse é o tempo que a velocidade angular leva para atingir .
Passo 4
Podemos igualar esses dois instantes de tempo para descobrir qual é a velocidade da bola quando ela começa a rolar sem deslizamento:
E podemos calcular o raio em função da circunferência:
Então:
E já que a aceleração sobre a bola é , qual a distância percorrida por ela até atingir essa velocidade?
Resposta
A distância percorrida será de .