Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 115b
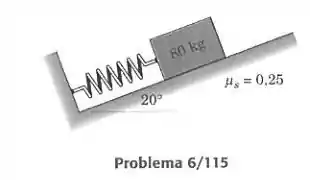
O bloco de 80 kg está colocado contra a mola em um plano com inclinação de 20° e é solto a partir do repouso. O coeficiente de atrito estático entre o bloco e o plano inclinado vale 0,25. Calcule o módulo e o sentido da força de atrito atuando sobre o bloco se a força de compressão da mola vale 200 N.
Passo 1
No item isolamos o corpo em diagrama de corpo livre para determinar na iminência de movimento do bloco. Vamos agora representar novamente o corpo, mas conhecendo a força . Agora, por não se tratar da iminência do movimento, o coeficiente de atrito não é o estático máximo 0,25, então não sabemos a relação entre a força de atrito e a força normal do solo.
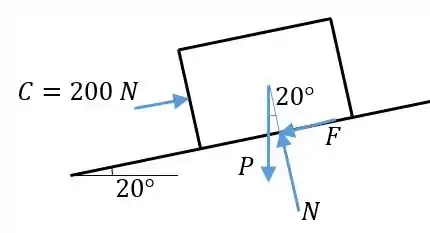
Passo 2
Fazemos as equações de equilíbrio, sendo a direção paralela ao plano. O peso do corpo é:
Então:
O sinal negativo indica que erramos o sinal de , que aponta na verdade para a direita, impedindo o bloco de descer.