Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 11

Calcule as forças nos elementos C G e C F para a treliça mostrada.

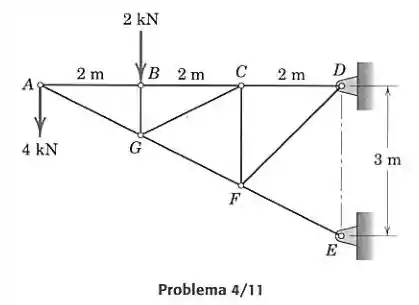
Passo 1

Vamos calcular as equações de equilíbrio para cada nó. C indica que o elemento está comprimido e T indica que ele está tracionado. Consideraremos todas as forças desconhecidas de tração, e se obtivermos um valor negativo quer dizer que são de compressão.

Precisamos conhecer o ângulo θ = G A ^ B = B C ^ G = 2 C G ^ F para calcular as equações desse nó. Por semelhança de triângulos do triângulo A D E com o A B G , podemos ver que:

B G - D E - = A B - A D - ⇒ B G - 3 = 2 6 ⇒ B G - = 1

Então, por Pitágoras:

A G - = 1 2 + 2 2 = 5

⇒ sen ⁡ θ = 1 5 ; cos ⁡ θ = 2 5

Passo 2

Agora temos para o nó D :

∑ F x = 0 ⇒ A B + A G cos ⁡ θ = 0 ⇒ A B = - A G cos ⁡ θ

Substituindo pelo valor de cos ⁡ θ :

A B = - 2 A G 5

∑ F y = 0 ⇒ - 4 - A G sen ⁡ θ = 0 ⇒ A G = - 4 sen ⁡ θ

Substituindo o valor de sen ⁡ θ :

A G = 4 5   k N   ( C )

Então:

A B = 4 5 ⋅ 2 5 ⇒ A B = 8   k N   ( T )

Passo 3

Nó B:

∑ F x = 0 ⇒ - A B + B C = 0 ⇒ B C = 8   k N   ( T )

∑ F y = 0 ⇒ - 2 - B G = 0 ⇒ B G = 2   k N   ( C )

Passo 4

Nó G:

∑ F x = 0 ⇒ A G cos ⁡ θ + C G cos ⁡ θ + F G cos ⁡ θ = 0

Dividindo tudo por cos ⁡ θ :

⇒ A G + C G + F G = 0 ⇒ F G = - A G - C G = 4 5 - C G

∑ F y = 0 ⇒ - 2 - A G sen ⁡ θ + C G sen ⁡ θ - F G sen ⁡ θ = 0

Substituindo sen ⁡ θ e F G pelo valor encontrado anteriormente:

⇒ - 2 - 4 5 ⋅ 1 5 + C G 5 + 4 5 + C G 5 = 0 ⇒ - 2 - 4 + C G 5 + 4 + C G 5 = 0

⇒ 2 C G 5 = 2 ⇒ C G = 5   k N = 2,25   k N   ( T )

Então:

F G = 3 5   k N   ( C )

Passo 5

Nó C:

∑ F y = 0 ⇒ C G sen ⁡ θ - C F = 0 ⇒ C F = C G sen ⁡ θ

Substituindo pelo valor do seno encontrado no passo 1 e pelo valor de C G = 5 :

C F = 5 ⋅ 1 5 ⇒ C F = 1,00   k N   ( T )

Resposta

C G = 2,25   k N   ( T )

C F = 1,00   k N   ( T )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o maior peso P 2 que pode ser aplicado à trelila de modo que a força em qualquer membro não exceda 2,5k N (T) ou 1,75k N (C). Considere P 1 = 0 .
Determine a força em cada membro da treliça e diga se os membros estão sob tração ou compressão. Faça P 1 = 1200N e P 2 = 500k N .
Remova as forças de 6k N e determine a maior força P que pode ser aplicada à treliça de modo que nenhum dos membros esteja sujeito a uma força que exceda 10k N em tração ou 7,5k N em compressão.
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. Faça P = 5k N
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.