Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 23
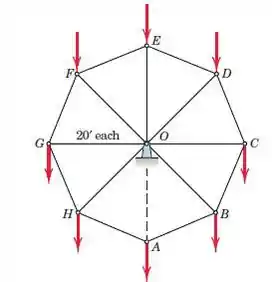
Uma pequena roda-gigante é construída com duas treliças idênticas, uma das quais é mostrada. O membro AO é temporariamente removido para substituição. Se o peso das cadeiras e membros estruturais resultar em uma carga de 100 lb em cada junta da treliça mostrada, determine a força em cada membro da estrutura. Com o membro AO substituído, você poderia repetir a análise?
Passo 1
Primeiro, se olharmos para a imagem, podemos ver que há 8 triângulos na roda e disso sabemos que o ângulo entre as linhas AO e BO (e todas as outras) é 45∘. Visto que seus lados têm o mesmo comprimento, sabemos que os outros ângulos no triângulo devem ser . Olhando para o ponto A, vemos que apenas as forças horizontais são componentes horizontais de AH e AB, portanto, devem ser iguais. Além disso, vemos que os componentes verticais dessas duas forças devem cancelar a força externa.
Passo 2
Agora olhamos para o ponto H e vemos que o ângulo entre OH e horizontal é 45 ∘ e daí também vemos que o ângulo entre AH e horizontal é 22,5∘. Além disso, o ângulo entre GH e vertical é 22,5∘. A partir de tudo isso, dividimos nossas forças nos componentes verticais e horizontais.
(vertical)
(horizontal)
Subtraindo, temos
Retornando isso à expressão para as forças verticais, obtemos:
Passo 3
Podemos prosseguir para o ponto G. A força externa atua em conjunto com o componente vertical do GH para anular o componente vertical do FG. Também os componentes horizontais das forças FG e GH têm que cancelar a força GO.
(vertical)
(horizontal)
Movendo-se para o ponto F, vemos que o ângulo entre FG e a vertical é 22,5 ∘ e que o ângulo entre FO e a horizontal é 45∘. Além disso, o ângulo entre FE e horizontal é de 22,5∘.FG está sendo puxado para baixo de modo que seu componente vertical junto com a força externa está cancelando os componentes verticais de FO e FE. Além disso, o componente horizontal de FG junto com o componente horizontal de FO deve cancelar o componente horizontal de FE.
(vertical)
(horizontal)
Passo 4
Subtraindo, temos
Retornando isso à expressão para as forças verticais, obtemos:
Finalmente, se olharmos para o ponto E, vemos que apenas as forças horizontais são componentes horizontais de EF e ED. Disto podemos concluir que os membros do lado direito devem ter forças iguais atuando sobre eles como seu par do lado esquerdo.
Passo 5
Por tudo isso, sabemos que a barra EO deve cancelar as componentes verticais da força EF e DE e da força externa.
Cada membro conectado ao ponto O está sendo encurtado por forças externas (compressão) e cada membro no aro está sendo alongado por forças externas (tensão). Se adicionássemos o membro AO de volta, a roda seria indeterminada.