Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 30
O vagão-plataforma de suporta um veículo de em uma rampa de construída sobre o vagão-plataforma. Se o veículo é liberado a partir do repouso com o vagão-plataforma também em repouso, determine a velocidade do vagão-plataforma quando o veículo tiver se deslocado para baixo na rampa logo antes de bater na trava em . Despreze todo o atrito e trate o veículo e o vagão-plataforma como partículas.
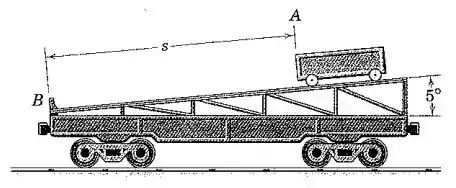
Passo 1
Como há conservação de energia no sistema, podemos escrever:
onde os índices e se referem ao vagão-plataforma e ao veículo, respectivamente.
Como a velocidade que o vagão adquire é , temos:
Para calcular , chamaremos de a velocidade de descida do veículo, relativamente ao vagão. Então, a velocidade do veículo tem duas componentes:
Lembrando que subtraímos de porque o veículo acompanha o movimento do vagão. Então:
Passo 2
Como o vagão não se movimenta verticalmente, temos:
Já o veículo desce uma altura de , logo:
Substituímos, então, todos os valores na equação de energia:
Usaremos essa equação mais tarde.
Passo 3
Note que também temos conservação da quantidade de movimento na direção , ou seja,
Inicialmente, tanto o vagão quanto o veículo estão em repouso. Mas, como já calculamos, o veículo adquire velocidade , e o vagão, (com sentido contrário à velocidade do veículo):
Passo 4
Agora que temos a expressão de em função de , podemos substituí-la nessa equação: