Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 83
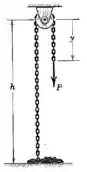
Determine a força necessária para dar a corrente de elos de comprimenro total uma velocidade constante . A corrente possui uma massa por unidade de comprimento. Além disso, pela aplicação da equação do impulso-quantidade de movimento à parte do lado esquerdo do sistema, verifique que a força que suporta a pilha de corrente é igual ao peso da pilha. Despreze o pequeno tamanho e massa da polia e qualquer atrito na polia.
Passo 1
Vamos definir o sentido positivo como aquele em que a corrente é puxada na direção da força , e o negativo é o caminho contrário.
Nesse caso, a soma das forças que agem sobre a corrente na direção vertical são as seguintes:
Onde é a força peso da porção da corrente que já está do lado direito da polia, e é a força de tração exercida pela parte esquerda da corrente.
Para que a corrente tenha velocidade constante todas essas forças tem que estar em equilíbrio:
Passo 2
Ok, mas temos uma equação com duas variáveis desconhecidas ( e ), e queremos determinar uma das duas. Precisamos achar uma segunda equação.
Vamos olhar para o lado esquerdo da corrente, e usar a equação que dá a força resultante externa:
E para o lado esquerdo, as duas forças externas aginso são o peso da parte que está suspensa e a tração, em sentidos opostos:
Nesse caso a tensão ficou com o sinal positivo porque estamos usando a mesma convenção de antes. E a força peso pode ser escrita como:
Como a corrente atinge uma velocidade constante, a aceleração é nula:
A massa da porção suspensa varia conforme a corrente sobe:
Então:
Beleza, encontramos uma segunda equação, agora ficamos com o seguinte sistema:
Subtraindo uma equação da outra:
E isso responde a primeira parte da questão.
Passo 3
Agora queremos aplicar a equação do impulso-quantidade de movimento para mostrar que a força que sustenta a pilha de corrente no chão é igual ao seu peso.
A equação é a seguinte:
Onde são as forças externas e é a quantidade de movimento. Vamos aplicar essa equação ao lado esquerdo da corrente.
Para as forças externas vamos ter dois grupos. Apontando para cima temos a tensão exercida pela outra parte da corrente e a força de sustentação da pilha (que é uma força normal)
Apontando para baixo temos o peso da parte suspensa mais o peso da parte que está no chão.
Então:
Passo 4
Agora vamos olhar para a quantidade de movimento da porção esquerda da corrente:
Onde desconsideramos a parte da corrente que está parada no chão, já que esta não tem quantidade de movimento.
Pela regra do produto:
Como a velocidade da corrente é constante, , e é a própria velocidade da corrente:
Agora vamos voltar à nossa equação inicial:
Precisamos isolar a força :
E usando a equação que escrevemos lá no passo para :
Que é exatamente a força peso da parte da corda que ainda está empilhada no chão.
Resposta
A força necessária é e a força que suporta a pilha é .