Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 40
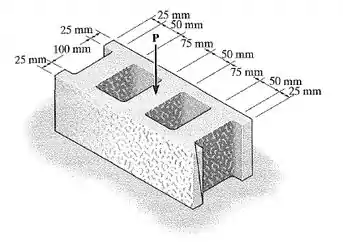
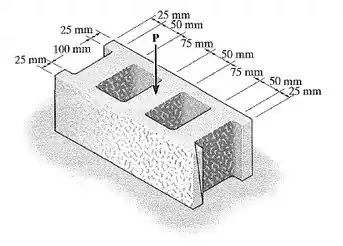
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suportar.
Passo 1
Oláaaa, meu querido, minha querida! Tá bem? Aqui temos:
Então, ele quer saber o maior valor de que esse bloco aguenta e ele dá a tensão normal média máxima .
Aí lembra que a tensão normal média é dada por:
Onde:
- é a tensão normal.
- a força normal na seção.
- a área da seção
Percebe que é a tensão normal a área da face horizontal do bloco. porque é a única força normal atuando ali. E ele dá as medidas para a gente achar , a área dessa face, e a tensão máxima média .
Por isso, podemos usar nossa expressão de tensão média para achar , assim:
Bora!
Passo 2
Primeiramente vamos calcular nossa área:
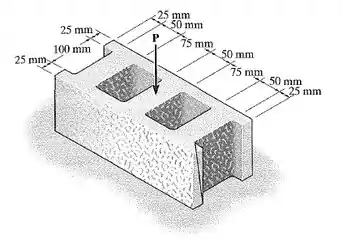
Primeiro vamos pensar em um bloco inteiriço e calcular a sua área, depois a gente subtrai a área das partes vazadas, beleza?!
Agora as áreas vazadas dos extremos:
E por fim os furos internos:
Então nossa área fica:
Passando para :
Passo 3
Já que temos a área a e tensão, podemos calcular a força P:
Colocando a tensão e a área no sistema internacional:
Substituindo na expressão de :
Passando para :