Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 32
A haste curvada AD de raio r tem peso por comprimento w. Se ela estiver no plano horizontal, determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B. Dica: A distância entre o centroide C do segmento AB e o ponto O é CO = 0,9745r.
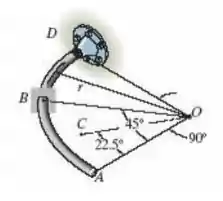
Passo 1
Primeiramente, devemos desenhar o diagrama de corpo livre para identificarmos os esforços.
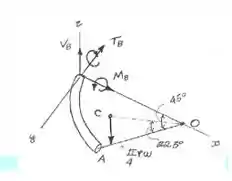
Sabemos que a única força atuante é o peso. Logo, devemos calcular o comprimento AB.
Podemos achar este coprimento utilizando a relação:
Agora, para acharmos o peso, podemos multiplicar o peso por comprimento pelo comprimento de AB.
Passo 2
Já temos a força atuante na seção, basta multiplicar pela distância até a seção para acharmos o momento fletor. Vamos considerar que o peso se concentra no meio de AB.
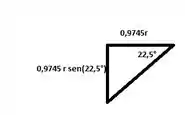
Repare que o sinal de menos significa que o sentido adotado no DCL não é o correto.
Passo 3
No caso do momento em y, temos que a distância ao eixo da peça é . Logo, multiplicando-se a força pela distância teremos o momento.
( =