Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 34
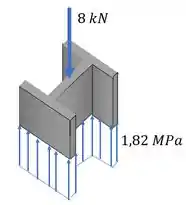
A coluna está sujeita a uma força axial de 8 kN aplicada no centroide da área da seção transversal. Determine a tensão normal média que age na seção a-a. Mostre como fica essa distribuição de tensão sobre a seção transversal da área.
Passo 1
Faaaala, querido! Ele quer a tensão normal média nessa seção. A fórmulinha da tensão normal média é
Onde é a carga normal/axial sobre essa seção, que ele diz valer:
E é área da seção. Percebe que nossa coluna é reta, então a área da seção é a mesma da área que a gente vê mais acima na figura. Podemos determinar essa área assim:
Como temos a força e a área da seção, a tensão é:
=
Repare que as unidades usadas foram o mm² e N, dando o resultado diretamente em MPa.
Passo 2
Neste caso, a tensão é distribuída uniformemente. Fica com a cara de uma carga distribuiida sobre toda a seção mesmo. E a gente achou o valor médio dela, então é uma carga distribuída com valor de .
Aí fica assim:
Repara que a gente fez um elemento representando a seção . E a tensão está virada para cima para que esse elemento fique em equilíbrio com a força aplicada acima.
Resposta
