Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 20

O bloco A de 5   k g desloca-se para a direita com v A = 0,6   m / s no instante mostrado. Se o coeficiente de atrito cinético entre a superfície e A é μ k = 0,2 , determine a velocidade de A quando ele se deslocou 1,2   m . O bloco B tem um peso de 100   N   ( m ≈ 10   k g ) .

Passo 1

Temos um problema que envolve polia! Começaremos analisando a cinética do problema, esboçando o diagrama de corpo livre, para despois partirmos para a parte de cinemática, relacionando as acelerações para que possamos resolver o nosso problema! Temos que tomar muito cuidado nesta última etapa!!!

Passo 2

Começaremos esboçando o diagrama de corpo livre dos nossos blocos. Ambos os blocos possuem um diagrama bastante semelhante, mudando apenas o valor da componente do peso. Sendo assim, temos:

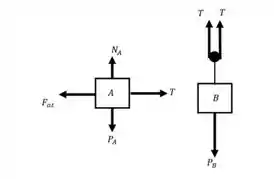
Para o bloco A temos:

← ∑ F x = m a A

F a t - T = m a A

N A μ k - T = m a A

5 ⋅ 9,81 ⋅ 0,2 - T = 5 a a

a A = 1,95 - 0,2 T

Já para o bloco B, temos:

↑ ∑ F y = m ⋅ a B

2 T - P = m ⋅ a B

2 T - 100 = 10 a B

a B = 0,2 T - 10

Passo 3

Devido a relação das polias, temos que a relação do deslocamento do bloco A com o bloco B é dado por:

s A + 2 s B = L

Diferenciando duas vezes, temos:

a A + 2 a B = 0

Portanto, teremos substituindo este valor nas equações da cinética, teremos:

a A = 1,95 - 0,2 T

a A = 20 - 0,4 T

Resolvendo este sistema, obtemos que:

a A = - 16,1   m / s 2

Portanto, a aceleração do bloco A é para a direita! Como a aceleração é constante, para um deslocamento de 1,2   m , teremos:

v 2 - v 0 2 = 2 a Δ s

v 2 - 0,6 2 = 2 ⋅ 16,1 ⋅ 1,2

v = 6,24   m / s

Resposta

v = 6,24   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força constante F que deve ser aplicada à corda a fim de fazer com que o bloco A de 15 kg tenha uma velocidade de 3,6m / s quando for deslocado 0,9m para cima partindo do repouso. Despreze
Um homem de 75 kg sobe a corda com uma aceleração de 0,25m / s 2 , medida em relação à corda. Determine a tração na corda e a aceleração do bloco de 80k g .
O eixo CA de 2 kg passa por um mancal radial liso em B. Inicialmente, as molas, que estão enroladas livremente em torno do eixo, não estão deformadas quando nenhuma força é aplicada ao eixo. Nesta pos
O bloco B tem massa m e é solto do repouso quando está no topo da carreta A que tem massa de 3m. Determine a tração na corda CD necessária para evitar que a carreta se desloque enquanto B escorrega pa