Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 23
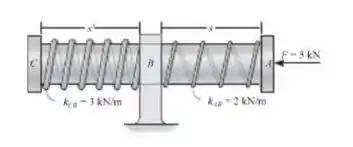
O eixo CA de 2 kg passa por um mancal radial liso em B. Inicialmente, as molas, que estão enroladas livremente em torno do eixo, não estão deformadas quando nenhuma força é aplicada ao eixo. Nesta posição e o eixo está em repouso. Se uma força horizontal é aplicada, determine a velocidade do eixo no instante que , . As extremidades das molas estão presas ao mancal em , e as tampas, em C e A.
Passo 1
Temos um problema que envolve molas! Portanto, vamos relembrar antes como calculamos a força de uma mola. Dada uma mola de constante elástica e deformada por um comprimento , a sua força é:
O problema quer que calculemos a velocidade do eixo após uma deformação de . Portanto, o eixo, o qual estará submetido a uma série de forças, será deslocado por . Precisamos aliar então as equações da cinética e da cinemática.
Passo 2
Vamos começar fazendo o diagrama de corpo livre do nosso eixo. Ele está sujeito a uma força causada pela mola CB, uma pela mola CB e outra pela própria força de . Portanto, temos:
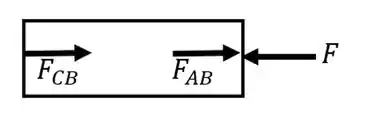
As forças das molas são dadas por:
Fazendo um somatório de forças em todo o eixo ao longo do eixo , temos:
Descobrimos agora uma função que relaciona a aceleração do eixo com a sua posição! Precisamos partir para a cinemática agora.
Passo 3
Agora que trabalhamos com a cinética, vamos voltar para a cinemática. Como obtemos a aceleração em função da posição, para descobrirmos a sua velocidade, utilizaremos a seguinte equação.