Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 21

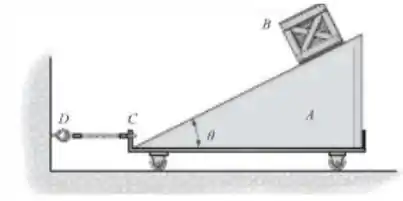
O bloco B tem massa m e é solto do repouso quando está no topo da carreta A que tem massa de 3m. Determine a tração na corda CD necessária para evitar que a carreta se desloque enquanto B escorrega para baixo em A. Despreze o atrito.

Passo 1

Precisamos determinar a tração na corda CD. Se a carreta não desloca, mesmo enquanto a caixa B cai, sabemos então que ela está parada. E não só isso! Como ela não se movimenta, consequentemente, o somatório de forças é igual a 0 – carreta não acelera! Portanto, para resolvermos esta questão, precisamos começar fazendo o seu diagrama de forças!

Passo 2

Vamos começar fazendo o diagrama de corpo livre da caixa B. A mesma está sujeita apenas a uma força normal e o peso. Consequentemente, temos:

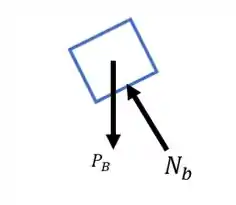
Como a força normal é capaz de contrabalancear uma componente da força peso, temos:

↖ ∑ F y = 0

N B - P B ⋅ cos ⁡ θ = 0

N B = m g cos ⁡ θ

Passo 3

Vamos analisar agora o diagrama de corpos livre da carreta. Temos então:

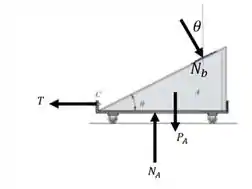
Temos a tração T da corda, as componentes normais N A da carreta e N B da caixa e o peso da carreta P A . Como a carreta está parada, temos uma aceleração, nula. Portanto,

→ ∑ F x = 0

- T + N B sen ⁡ θ = 0

T = N B sen ⁡ θ

Como descobrimos a intensidade da força N B , temos:

T = m g cos ⁡ θ sen ⁡ θ

Resposta

T = m g cos ⁡ θ sen ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motor de 3,5 Mg está suspenso por uma viga transversal A B de massa desprezível e é içado por um guindaste que exerce uma força de 40 kN no cabo de içamento. Determine a distância pela qual o motor
O motor de 3,5 Mg está suspenso por uma viga transversal A B de massa desprezível e é içado por um guindaste que dá a ele uma aceleração de 4 m / s 2 quando ele tem uma velocidade de 2 m / s . Determi
O homem empurra a caixa de 30 kg com uma força F . A força é sempre direcionada para baixo a 30 0 da horizontal, como mostrado, e sua intensidade é aumentada até a caixa começar a deslizar. Determine
Os blocos A e B têm massa de m A e m B , sendo m Am B . Se é dada uma aceleração de a 0 para a polia C, determine a aceleração dos blocos. Despreze a massa da polia.
Se a força do motor M sobre o cabo é mostrada no gráfico, determine a velocidade do carrinho quando t = 3s . A carga e o carrinho têm massa de 200k g e o carrinho parte do repouso.