Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 20
O bloco e a haste anexa têm, juntos, uma massa de e estão limitados a se deslocar ao longo da guia de sob a ação da força aplicada de . A haste uniforme horizontal possui uma massa de e está soldada ao bloco em . O atrito na guia é desprezível. Calcule o momento fletor exercido pela solda sobre a haste em .
Passo 1
Quando o conjunto inteiro sobe ao longo da guia de com uma aceleração , qual é a força resultante que age sobre a viga horizontal de massa (no seu centro de massa)?
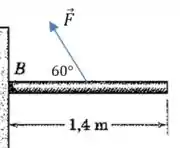
E qual é o torque exercido por essa força? Vamos tomar como referência a extremidade direita da viga:
Isso quer dizer que quando calcularmos o momento total das forças que agem sobre a viga, devemos ter:
Passo 2
E quais são essas forças que produzem momento sobre a viga? Temos o momento fletor que queremos calcular, e o momento da força peso que age no centro de massa da viga:
O momento aponta no sentido anti-horário porque ele impede que a viga gire no sentido horário ao cair.
E igualando isso ao resultado que tínhamos encontrado no passo anterior:
Agora só falta encontrar a aceleração do sistema para poder calcular .
Passo 3
Dê uma olhada na figura do enunciado. A aceleração do sistema de massa será ao longo da guia, certo? Vamos analisar a soma das forças nessa direção:
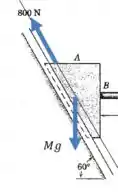
Agora vamos substituir na nossa equação de antes (lembre de distinguir entre a massa da viga e a massa do sistema inteiro):
Resposta
O momento fletor exercido pela solda sobre a haste é .