Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 7

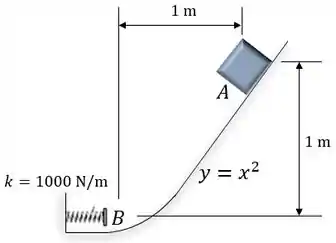
O bloco de 3 kg é solto do repouso em A e escorrega para baixo pela superfície parabólica lisa. Determine a compressão máxima da mola.

Passo 1

O enuncia nos dá a seguinte informação:

Massa do bloco:   m = 3 kg;

Constante elástica da mola: k = 1000   N / m ;

Superfície parabólica: y = x 2 ;

Superfície lisa: desprezar o efeito do atrito.

Devemos determinar a compressão máxima da mola em B quando o bloco é solto do repouso em A .

Desenhamos o diagrama de corpo livre do bloco em B :

Vamos considerar dois momentos:

No momento (1), o bloco está em repouso e ainda não se deslocou, logo

v 1 = 0  

s 1 = 0

No momento (2), o bloco atinge a mola e a comprime até seu ponto máximo, logo

v 2 = 0

s 2 = s

Aqui consideraremos o trabalho de um peso ( U W = W y ) , representado pelo produto da intensidade do peso e o deslocamento vertical. Ele é positivo quando o peso se desloca para baixo. Além dele, temos o trabalho da mola ( U s = 1 2 k s 2 ) , porém, este terá sinal negativo pois a força da mola age no sentido oposto à direção do movimento.

Através do diagrama, vemos que N = W = m g .

Passo 2

Vamos aplicar o Princípio do Trabalho e da Energia:

T 1 + ∑ U 1 - 2 = T 2

Onde

T 1 = 1 2 m v 1 2 = 1 2 m 0 = 0

T 2 = 1 2 m v 2 2 = 1 2 m 0 = 0

∑ U 1 - 2 = U W + U s = ( 3 ) g 1 - 1 2 ( 1000 ) s 2

Substituindo esses valores na equação principal, obtemos

0 + 3 g - 1 2 ( 1000 ) s 2 = 0

1 2 1000 s 2 = 3 g

s = 0,2426   m

Resposta

s = 0,243   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco A tem massa de 0,75 kg e desliza na ranhura horizontal lisa. Se o bloco é recuado para s=0,45 m e solto do repouso, determine sua velocidade no instante s=0. Cada uma das duas molas tem uma ri
Cada uma das duas tiras de elástico do estilingue tem um comprimento não deformado de 200mm. Se elas são puxadas para tras para a posição mostrar e soltas do repouso, determine a velocidade do chumbin
Resolva o problema 14.22 utilizando a equação de conservação da energia.
O bloco A de 1 kg desliza na fenda horizontal lisa. Quando s=0, o bloco é submetido a uma velocidade incial de 18 m/s para a direita. Determine o deslocamento horizontal máximo s do bloco. Cada uma ds
O movimento de um barco de 3250 kg é impedido usando-se um para-choque que proporciona uma resistência como mostrado no gráfico. Determine a distância máxima que o barco amassa o para-choque se a sua