Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 2
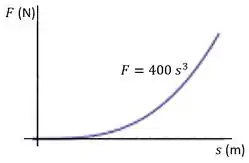
O movimento de um barco de 3250 kg é impedido usando-se um para-choque que proporciona uma resistência como mostrado no gráfico. Determine a distância máxima que o barco amassa o para-choque se a sua velocidade de aproximação é 0,9 m/s.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do barco: ;
Velocidade de aproximação do barco: .
Devemos determinar a distância máxima que o barco amassa o para-choque.
No ponto em que o barco atinge a distância máxima, sua velocidade será igual à zero (). Pense que o para-choque funciona como um amortecedor que absorve a energia do movimento do barco.
Passo 2
Sabemos que o trabalho realizado por uma força é igual a área sob o gráfico Força-Deslocamento.
Neste caso, a Força agirá no sentido oposto ao deslocamento, pois ela tentará parar o barco, sendo uma força de resistência. Logo, o trabalho realizado por ela será negativo.
Além disso, quando o barco atinge a distância máxima, sua velocidade neste instante será igual à zero ().
Aplicando o Princípio do Trabalho e Energia, temos
Onde o instante (1) representa o momento em que o barco toca o para-choque e o instante (2) representa o momento de deslocamento máximo que o barco amassa o para-choque.
Temo que,
Substituindo estes valores na equação, obtemos