Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 76
Resolva o problema 14.22 utilizando a equação de conservação da energia.
Passo 1
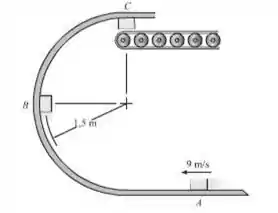
Utilizando a equação da conservação da energia de A a B, teremos
Substituindo os dados do problema
Para o calculo da força Normal em B, devemos fazer o DCL da caixa em B
Passo 2
Utilizando a equação da conservação da energia de A a C, teremos
Substituindo os dados do problema
Para o calculo da força Normal em B, devemos fazer o DCL da caixa em B
Resposta
A velocidade e a força normal em B são, respectivamente 7,18 m/s e 34,37 N
A velocidade e a força normal em C são, respectivamente 4,70 m/s e 14,73 N
Exercícios de Livros Relacionados
3/122) A resistência R à penetração x de um projétil de 0,25k g disparado com uma velocidade de 600m / s em um bloco de material fibroso é apresentada no gráfico . Represente essa resistência pela lin
3/129) O pequeno cursor de massa m é liberado a partir do repouso quando na posição A e então desliza ao longo da pista no plano vertical. A pista Elisa de A até D e rugosa .(coeficiente de atrito din
3/139) A força P = 40N é aplicada ao sistema , que está inicialmente em repouso . Determine as velocidades de A e B após A ter se deslocado 0,4m .
3/141) Em um teste de projeto da pressão no anel de segmento , o pistão especial de alumínio com 100m m de diâmetro com uma massa de 2,7k g é liberado a partir do repouso no cilindro vertical sob a aç
3/138) O jogo de duas molas é usado para trazer o êmbolo A de 0,5k g para o repouso a partir de uma velocidade de 5 m / s e inverrter o seu sentido de movimento . A mola internaaumenta a desaceleração