Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 18

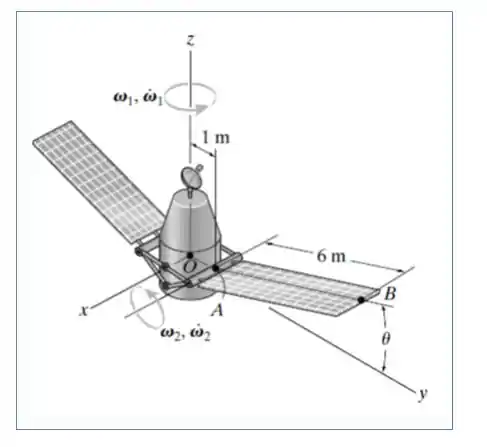
No instante θ = 0 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 20   r a d / s , e tem uma aceleração angular   ω ˙ 1 = 5   r a d / s ² . No mesmo instante, o satélite se desloca na direção x com uma velocidade v o = 5000   i   m / s , e tem uma aceleração a o = 500   i   m / s ² . Simultaneamente, os painéis solares giram com uma velocidade angular ω 2 = 5   r a d / s . Determine a velocidade e a aceleração do ponto B localizado na extremidade de um dos painéis solares nesse instante.

Passo 1

Definir os vetores de velocidade:

Ω = 20   k   r a d / s

ω ˙ 1 = 5 k   r a d / s  

E a velocidade e aceleração do ponto A.

V a = v o + ω ˙ 1   x   r O A = 5000   i + 20 k   x   1 j =   - 4980 i   m / s

  a A =   a o + ω ˙ 1   x     r O / A + ω 1   x ( ω 1   x   r O A   )

= 5000 i +   5 k   x   1 j   +   20 k   x   ( 20 k   x   1 j )

=   - 495 i   – 400 j   m / s ²

Passo 2

Para determinar o movimento B relativo ao A, é nesessário um segundo eixo de referências que coincide com o eixo xyz, chamaremos de x’y’z’.

Assim:

V b / a   =   r ˙ b / a = ( r ˙ ( b / a ) x ' y ' z ' +   ω 2   x   r b / a )

=   0   +   5 i   x   ( 6 c o s 30 ° j + 6 s i n 30 ° k )

=   - 15 j + 25,98 k   m / s

Passo 3

Encontrar   a b =   ω ˙ 2 = 0 logo não há aceleração:

Resposta

Assim a velocidade no ponto B é de - 15 j + 25,98 k   m / s e sua aceleração é 0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante θ = 30 ° , a estrutura do guindaste e a lança A B está girando com uma velocidade angular constante ω 1 = 1,5r a d / s e aceleração angular ω ˙ 1 = 0,5r a d / s 2 , equanto a lança A B gir
Quando a barra A B está na posição mostrada, o anel A se desloca com uma velocidade v A = 5 im / s e aceleração a A = 1 im / s 2 . Determine a aceleração do anel B nesse instante. Suponha que a veloci
No instante θ = 30 ° , a estrutura do guindaste e a lança A B giram com uma velocidade angular constante ω 1 = 1,5r a d / s e ω 2 = 0,5r a d / s , respectivamente. Determine a velocidade e a aceleraçã
No instante mostrado, a base do braço robótico gira em torno do eixo z com uma velocidade angular ω 1 = 4 r a d / s , a qual está aumentando a ω ˙ 1 = 3r a d / s 2 . Além disso, a lança B C gira com u
Se a manivela B C gira com uma velocidade angular ω B C = 6r a d / s , determine a velocidade do anel em A . Suponha que a velocidade angular de A B é perpendicular à barra.