Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 80

O bloco A de 1 kg desliza na fenda horizontal lisa. Quando s=0, o bloco é submetido a uma velocidade incial de 18 m/s para a direita. Determine o deslocamento horizontal máximo s do bloco. Cada uma ds duas molas tem uma rigidez k= 2500 N/m e um comprimento não deformado de 0,15 m

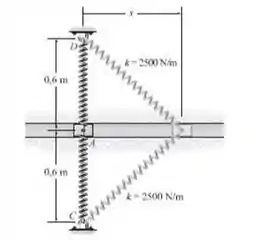
Passo 1

Utilizando a equação da conservação de energia, teremos

T 1 + V 1 = T 2 + V 2

1 2 m v 1 2 + 2 * 1 2 k x 1 2 = 0 + 2 * 1 2 k x 2 2

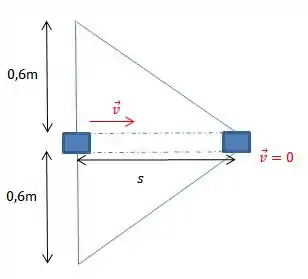
Como ao chegar no final do percurso, o bloco não possui velocidade, não haverá energia cinética no final. Precisamos agora encontrar quais são as nossas deformações nas molas.

No início teremos que a deformação é dada por:

x 1 = d 1 - 0,15

Sendo d 1 o comprimento da mola, e 0,15 o comprimento da mola relaxada, temos então:

x 1 = 0,6 - 0,15 = 0,45

E no final a nossa deformação vai ser dada por:

x 2 = d 2 - 0,15

Não sabemos quanto vale esse comprimento final da mola, mas se o encontrarmos poderemos encontrar o deslocamento horizontal do bloco (que é o que a questão pediu!). Pois temos a seguinte relação:

d 2 2 = 0,6 2 + s 2

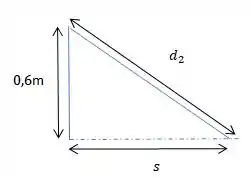
Então, bora encontrar esse d 2 aí!!

Passo 2

Substituindo os valores na nossa equação da energia, teremos:

1 2 m v 1 2 + 2 * 1 2 k x 1 2 = 0 + 2 * 1 2 k x 2 2

1 2 ( 1 ) ( 18 ) 2 + 2 [ 1 2 ( 2500 ) ( 0,45 ) 2 ] = 0 + 2 [ 1 2 ( 2500 ) ( d 2 - 0.15 ) 2 ]

Resolvendo os calculos, teremos

162 + 506,25 = 2500 d 2 2 - 0,3 d 2 + 0,0225

668,25 = 2500 d 2 2 - 750 d 2 + 56,25

2500 d 2 2 - 750 d 2 - 612 = 0

d 2 - 0,3 d - 0 , 244 = 0

Resolvendo a equação de 2° grau

d = 0 , 67 m

Então será

d 2 2 = 0,6 2 + s 2

s 2 = 0,67 2 - 0,6 2

s 2 = 0,084

s = 0,29 m

Resposta

O deslocamento horizontal máximo será 0,29 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/140) O cilindro de 6k g é liberado a partir do repouso na posição mostrada e cai sobre a mola , que foi inicialmente pré-comprimida em 50m m pela trava leve e fios restritivos . Se a rigidez da mola
3/142) Ensaios extensivos de um automóvel experimental de 900k g revelaram a força de arrasto aerodinâmico F A e a força total não aerodinâmica de resistência ao rolamento F R serem como mostrado no g
O carro de massa m acelera em uma estrada horizontal sob a ação da força motriz F de uma velocidade v 1 até uma velocidade mais alta v 2 em uma distância s . Se o motor desenvolve uma potência de saíd
O bloco de 10k g é liberado a partir do repouso sobre a superfície no ponto B , onde a mola foi esticada por uma distância de 0,5m a partir de sua posição neutra A . O coeficiente de atrito dinâmico e
Um menino de 40k g parte do repouso na base A de uma inclinação de 10 % e aumenta sua velocidade em uma taxa constante até 8k m / h quando passa em B , 15m ao longo da inclinação a partir de A . Deter