Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 142
Sabendo que dois topos iguais foram removidos da esfera de madeira de diâmetro 250 mm, determine a área total da superfície da parte restante.
Passo 1
Pra começar podemos desenhar a linha que será rotacionada para formar a superfície dada, então, temos:
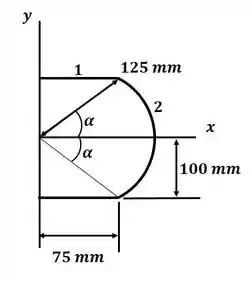
Então, podemos calcular a área da superfície através da fórmula vista nessa seção:
Passo 2
Então, precisamos descobrir o valor de , para isso precisamos do ângulo , que será dado por:
Convertendo esse valor para radianos, temos:
Agora, o valor de é dado por:
Então, o comprimento do arco será:
Passo 3
Agora podemos usar a fórmula da área do passo 1, substituindo os valores, temos:
E, resolvendo a expressão, temos:
Resposta
Exercícios de Livros Relacionados
O cilindro de concreto sólido com 6 pés de comprimento e 4 pés de largura diâmetro é apoiado em uma posição semi-submersa em água doce por um cabo que passa sobre um polia em A. Calcule a tensão T no
A seção transversal de um tanque de água doce com um fundo inclinado é mostrado. Uma porta retangular de 1,6 m por 0,8 m (normal ao plano da figura) no fundo do tanque é articulado em A e é aberto con
Os lados de uma calha de água doce em forma de V, mostrado na seção, são articuladas ao longo de sua interseção comum através de O e são apoiadas em cada lado por escoras verticais articuladas em cada
Determine a força total R exercida sobre a janela triangular pela água doce no tanque. O nível da água coincide com o topo da janela. Determine, também, a distância H , desde R até o nível da água.
A seção transversal mostrada representa um corpo de revolução, em torno do eixo z , de uma peça fabricada em ferro fundido. Calcule sua massa m .