Se o bloco pesa e o bloco pesa , determine o peso do bloco e do ângulo para o equilíbrio.
Passo 1
Falaaaa galerinha bonita do RespondeAí, bora lá fazer esse exercício deliciinha? Partiu!
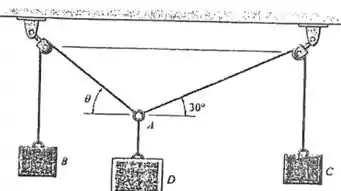
Saca só, o enunciado nos fornece blocos conectadas através de cabos e polias como no diagrama a seguir:
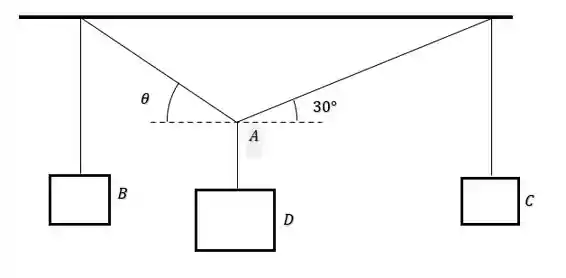
O enunciado continua nos dizendo que se o bloco pesa e o bloco pesa , então é pra gente encontrar o peso do bloco e do ângulo para o equilíbrio.
Passo 2
Iradoso galerinha, então se a gente desenhar as forças que atuam no sistema, vamos ter que:
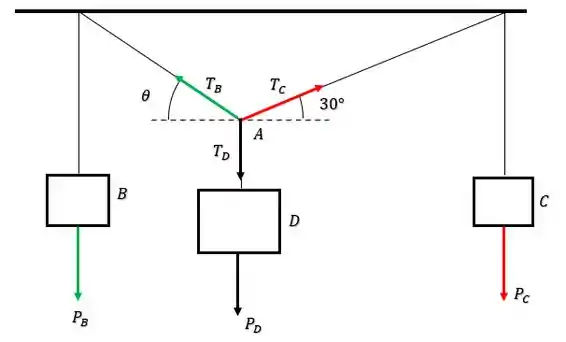
Onde as tensões em cada corda são geradas pelos respectivos pesos , de modo que quando falamos em módulo, teremos que:
Belezinha, vamos lá! Agora pensa aqui comigo: no equilíbrio, esses componentes do sistema não se mexem. Inclusive o ponto . Então vamos dizer que ele está em equilíbrio. Ou seja, no ponto :
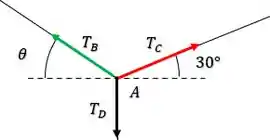
Isso quer dizer que se a gente conseguir encontrar o valor da tensão , estaremos encontrando a intensidade do peso do bloco .
Passo 3
Então belezinha pessoal, pra gente poder escrever as equações do equilíbrio, precisamos decompor as forças em cada eixo. Primeiro para a tensão , teremos que:
Para a tensão temos que:
E para a tensão , como ela está somente na vertical, teremos que:
Meczada, agora se a gente fizer a soma no eixo , vamos ter que:
Como está no sentido negativo, teremos que:
Logo, isolando :
Agora para o eixo , teremos:
Como está no sentido negativo do eixo , teremos:
Passo 4
Iradoso, mas se a gente substituir o valor de que encontramos nessa equação vamos obter um sistema muito complicado, MAAASSSSSSS, como a gente é malandro desde sempre, vamos lembrar lá do capítulo anterior e da Lei dos Cossenos, afinal podemos montar um triângulo com as forças, dado como:
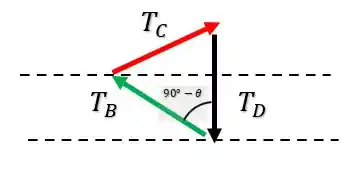
Agora podemos aplicar a lei dos cossenos para de acordo com o ângulo .

Logo:
Como , e o enunciado nos deu os valores de e , vamos obter que:
E como vimos que:
Então será dado como:
E como a relação trigonométrica fundamental nos diz que , então:
Igualando com a relação , vamos ter que:
Reorganizando:
Então se a gente fizer , teremos a seguinte equação do segundo grau:
E se a gente resolver essa equação, vamos encontrar as raízes:
Então por enquanto temos dois ângulos possíveis para , dados como:
Logo:
Passo 5
Belezera, agora se a gente substituir esses dois ângulos na equação para :
Para , vamos obter:
Agora para :
Maravilha, temos duas respostas possíveis, MAAAASSSSS, pra saber qual delas é a certa, precisamos testar na nossa equação para o eixo , dada como
A combinação que respeitar essa equação, vai ser nossa resposta certa.
Belezinha, testando para , teremos:
E por muito pouco vamos ter:
De modo que essa não é a resposta certa. Agora para a segunda combinação de , vamos obter:
Então nossa resposta certa será para , de modo que: