Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 43
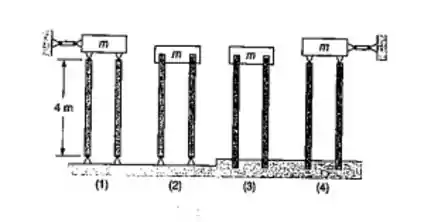
Um bloco rígido de massa m pode ser suportado por duas colunas, em um dos quatro modos mostrados. Cada uma das colunas consiste de um tubo de alumínio que tem um diâmetro externo de 44mm e uma espessura de 4mm. Usando E=77GPa e um coeficiente de segurança de 2,8, determinar a carga admissível para cada uma das condições de apoio.
Passo 1
E aí, vamos analisar umas estruturas?
Esse exercício traz pra gente o conceito de coeficiente de flambagem e ele vai entrar no comprimento efetivo do peso crítico:
E o peso crítico alterado fica:
Aqui temos 4 casos desse, temos que avaliar pelas tabelas que o livro traz que tipo de flambagem a gente tem para cada caso, encontrando o de cada um deles. Como a seção transversal é a mesma vamos primeiro encontrar os valores de e depois cada um dos pesos críticos.
Vamos analisar a figura, e analisar que tipo de vinculação cada coluna tem:
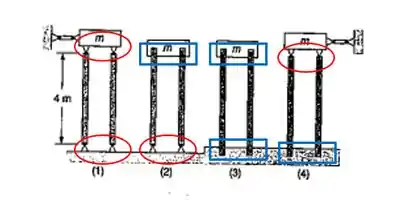
Em vermelho foram marcadas as vinculações do tipo apoio, e em azul as vinculações do tipo engaste. Sendo assim, temos para cada coluna:
- É bi-rotulada, e segundo o livro esse tipo de vinculação possui coeficiente de flambagem
- É rotulada numa extremidade e engastada na outra, e o coeficiente de flambagem nesse caso é .
- É bi-engastada, e segundo o livro esse tipo de vinculação possui coeficiente de flambagem
- É como a coluna 2, porém com posições trocadas sendo assim possui
A partir daqui vamos relacionar cada peso crítico com o peso admissível da coluna usando:
Passo 2
Vamos ao peso crítico mas antes vale trazer rapidinho o DCL que vale para todas as colunas, aqui vamos considerar genericamente dois apoios nas extremidades pois só nos interessam as reações verticais.
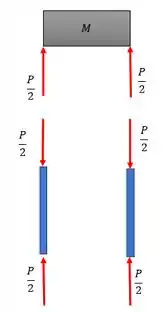
Lembrando que:
E nesse caso cada coluna possui:
Vamos agora atrás do momento de inércia da seção que é o que falta para o calculo do peso crítico e como a seção é vazada temos:
Passo 3
Agora, sem enrolação vamos ao cálculo do peso crítico, vamos usar nossa formulinha:
Vamos começar pela coluna 1, e para as outras basta a gente dividir por de cada coluna já que temos para a primeira .
E para a segunda coluna a gente vai ter:
E substituindo:
E para a terceira, temos:
E substituindo temos:
E por fim a coluna 4, que possui o mesmo coeficiente de flambagem da coluna 2, e nesse caso podemos dizer que:
Passo 4
Definidos os pesos críticos, vamos ao peso admissível, começando pela coluna 1:
E como vimos no passo 2:
Rearrumando:
E substituindo:
E como:
Substituímos o valor de P, em Kilonewtons e usamos .
Para a segunda e quarta colunas teremos a mesma massa pois tem as mesmas condições, então:
E novamente:
Substituímos:
E por fim:
Por último, temos a terceira coluna:
E como fizemos para as outras:
Daí:
E fazemos: