Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 4

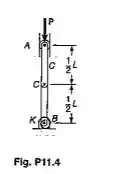
Duas barras rígidas AC e BC são conectadas por um pino C, como mostrado. Sabendo-se que a mola de torção em B é de constante k, determinar a carga crítica Pcr para o sistema.

Passo 1

Fala galeeera, bora pra mais uma?

A meta é relacionar esse peso P na coluna com algumas dimensões que geralmente são dadas, tipo o comprimento da coluna e a constante da mola e vamos chamar isso de peso crítico. A gente vai começar fazendo um diagrama da coluna inteira, sem separar e vamos achar algumas relações importantes.

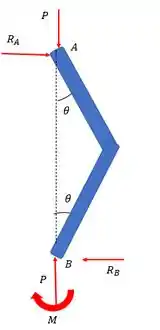
Vamos aqui escolher um ponto importante para eliminarmos incógnitas.

Passo 2

Usando o somatório dos momentos fletores em B a gente tem que:

∑ M B = R A L - M B = 0

Lembrando que:

M B = k θ

E aí:

R A = k θ L

Olhando agora para a barra AC separada a gente vai ter:

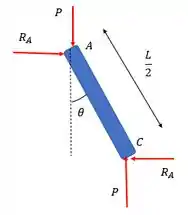
E pelo somatório dos momentos em C a gente encontra pro sentido horário positivo.

∑ M C = R A L 2 - P L 2 s e n θ = 0

R A s e n θ = P

E lembrando que como esse tipo de distorção angular é pequena a gente pode dizer que:

s e n θ ≅ θ

Substituindo RA, temos:

k θ L θ = P

E enfim:

P = P C R = k L

Resposta

P C R = k L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

10.7 A barra rígida AD está conectada a duas molas de constante k e está em equilíbrio na posição indicada. Sabendo que as cargas iguais e opostas P e P’ permanecem horizontais, determine a intensidad
10.22 Uma barra de alumínio quadrada de 25,4mm de lado é mantida na posição mostrada na figura por um apoio articulado em A e por conjuntos de roletes em B e C que impedem a rotação da barra no plano
10.20 Os elementos AB e CD são barras de aço com 30mm de diâmetro, e os elementos BC e AD são barras de aço com 22mm de diâmetro. Quando o tensor é acionado, o elemento diagonal AC é colocado sob traç
10.18 Um elemento de compressão com 8,2m de comprimento de flambagem é obtido ligando-se dois perfis U de aço U200 x 17,1 com barras de travejamento conforme mostra a figura. Sabendo que o coeficiente
A barra uniforme AB de latão tem seção transversal retangular e é suportada por pinos e suportes conforme mostrado. Cada extremidade da barra pode rotacionar livremente em relação ao eixo horizontal a