Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 45
A barra uniforme de alumínio AB tem uma seção transversal retangular de 20x30mm e é suportada por garfos e pinos, como mostrado. Cada uma das extremidades da barra pode girar livremente em torno de um eixo horizontal ao longo do pino, mas a rotação em torno de um eixo vertical é impedida pelos garfos. Usando-se E=200GPa, determinar a carga centrada admissível P, se um coeficiente de segurança de 2,5 é desejado.
Passo 1
E aí, vamos pra mais um de flambagem?
Esse exercício traz pra gente o conceito de coeficiente de flambagem e flambagem para dois planos diferentes aqui a chave pra resolver é analisar o que acontece em cada eixo de flambagem, então vamos desenhar:
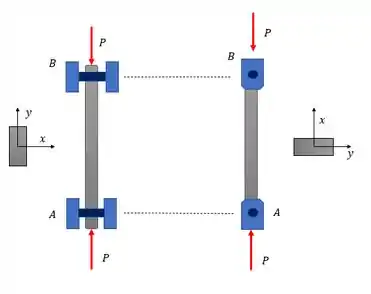
Olhando o nosso desenho a gente pode analisar bem as condições de contorno. Pra disposição da esquerda a rotação aparece impedida e os pinos vão travar a barra como engaste. Para a disposição da direita os pinos permitem a alguma rotação. Olhando as seções transversais de cada figura a gente vê que a possibilidade de girar em torno de é bem maior então temos que analisar os dois eixos e avaliar qual é o eixo fraco.
Definidos nossos parâmetros vamos avaliar o eixo fraco usando um outro parâmetro chamado de índice de esbeltez que é dado por:
O maior índice de esbeltez vai nos dar o eixo mais fraco.
Onde:
E:
E depois calcularemos o peso crítico usando:
E por fim o peso admissível com a relação:
Passo 2
Então vamos definir agora o que a gente vai usar para cada caso, a figura da esquerda possui dois engastes então:
E pela seção transversal a gente vê que pra esse eixo:
A figura da direita possui dois pinos, então:
E para esse eixo pela seção transversal vemos que:
Então vamos calcular a geometria da seção para definirmos o índice de esbeltez:
A área é dada por:
E o momento de inercia de cada eixo é:
Então para cada eixo o raio de giração é:
Enfim vamos avaliar qual o maior índice de esbeltez, para temos a disposição da esquerda que possui .
E para com
Então o eixo é o eixo fraco agora podemos calcular o peso crítico para esse eixo.
Passo 3
Calculando enfim o peso crítico para , temos:
Substituindo:
E enfim lembrando que: