Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 5
A barra rígida AD é fixa a duas molas de constante k e está em equilíbrio na posição mostrada. Sabendo-se que as cargas P e P' são iguais e opostas e permanecem verticais, determinar a intensidade PCR da carga crítica para o sistema. Cada uma das molas pode atuar tanto a tração quanto a compressão
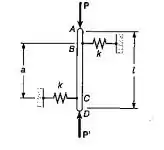
Passo 1
Vamos desenhar o nosso diagrama de corpo livre e tentar imaginar o que acontece com a barra quando são aplicadas as forças P nelas, ok?
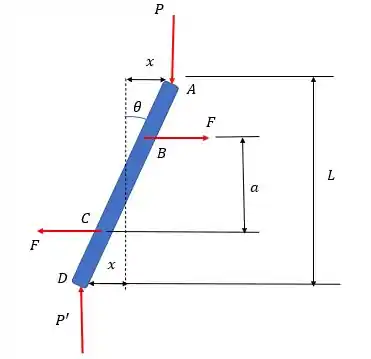
Repare que as molas vão reagir, e mesmo assim vai rolar uma distorção angular . Nossa meta é encontrar uma relação entre P e os elementos na figura, esse é o Pcrítico que leva a flambagem e qual é o pulo do gato pra resolver a questão? Essa figura aqui!
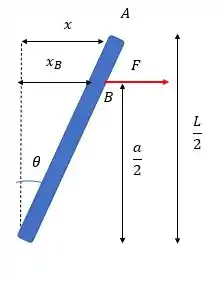
Na posição de cada mola vai rolar um deslocamento e aqui eu cortei a metade de cima da barra mas o que vai rolar em baixo é idêntico já que as forças são simétricas e são dadas por:
Passo 2
Da nossa figurinha a gente pode tirar do triângulo a seguinte relação:
E como a figura é simétrica a gente vai ter:
Vamos enfim partir pra relacionar P com toda a galera pois agora temos todas as distâncias. Fazendo o somatório dos momentos em D considerando o sentido horário positivo a gente tem:
Aqui vale dizer que você pode usar tanto a distância reta quanto a inclinada para a distância das forças F, pois o ângulo é tão pequeno que:
Detalhe que aqui a gente pode observar que as forças F formam um binário e portando o momento de binário foi calculado dessa forma:
Sendo que a distância entre eles era a.
Rearrumando a gente tem:
O sentido do binário foi adotado horário, porém o sinal deu negativo o que significa que o sentido do binário é contrário ao da figura, daqui em diante manteremos o sinal de P positivo e a gente pode fazer uma correção na figura trocando o sentido de cada força. Daí:
Onde:
Substituindo os valores:
E enfim: