Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 8
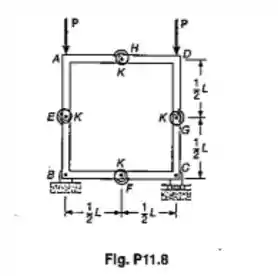
Um quadro consiste de quatro membros em forma de L,conectadas por quatro molas de torção, cada uma de uma constante k. Sabendo-se que iguais forças P são aplicadas nos pontos A e D, como mostrado, determinar a carga crítica Pcr para o sistema.
Passo 1
Fala aí, sei que esse problema tem uma cara assustadora mas não é nenhum bicho de sete cabeças não, prometo que ele vai ficar mais fácil. Vamos começar fazendo o diagrama de corpo livre, e para isso vamos separar todas as barras e analisar só uma delas.
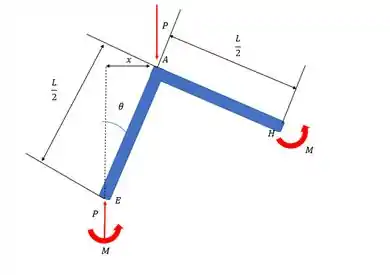
Repare que há momentos nas extremidades causados pelas molas.
A nossa meta aqui é encontrar o peso crítico que é o peso para o qual a peça está na iminência da falha, na nossa língua é o peso relacionado as dimensões e parâmetros do problema e que sai pelas equações de equilíbrio.
Passo 2
Vamos agora definir os nossos parâmetros e então fazer uma equação de equilíbrio dos momentos para encontrar P. Olhando a figura a gente vê a seguinte relação para x:
E como esse tipo de ângulo é bem pequeno podemos dizer que:
Daí x:
Beleza, mas quem é M?
M é dado pela relação:
Nesse caso, a mola tem a liberdade de girar e portanto a relação conhecida sofreu essa alteração.
Enfim escolhendo o ponto E para o somatório dos momentos e fazendo de positivo o sentido anti-horário, temos:
E isolando P:
Enfim substituindo x: