Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 30

O bloco está sujeito às duas cargas axiais mostradas figura. Determine a tensão normal desenvolvida nos pontos A e B . Despreze o peso do bloco.

Passo 1

Um bloco é comprimido por duas forças. Queremos saber o valor da tensão normal nos pontos A e B .

Primeira coisa a fazer é nos organizarmos e definirmos eixos com direções positivas. Veja a figura.

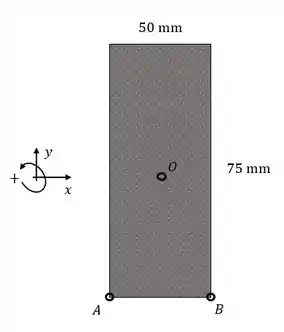
A força de 500   N atua na direção - z sobre B .

A força de 250   N está no vértice superior esquerdo, apontando para a direção - z .

Vamos calcular os esforços na seção transversal que contém A e B .

Passo 2

O equilíbrio de forças é tranquilo. A normal N vai apontar para z e equilibrar os carregamentos.

∑ F z = 0       →         N = 500   N + 250   N = 750   N

Esse esforço vai comprimir a seção!

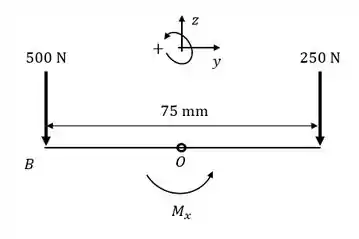
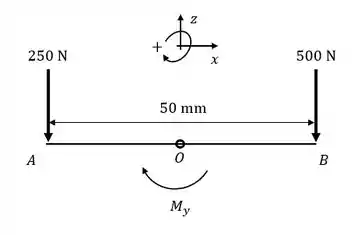
Vejamos o equilíbrio de momentos ao redor do ponto O . Temos dois eixos para checar.

Para o eixo x , considere um momento interno M x na direção positiva ( + x ) .

∑ M 0 x = 0       →         M x + 75 2   mm ⋅ 500   N - 75 2   mm ⋅ 250   N = 0

M x = - 9,375   Nm

Para o eixo y , considere um momento interno M y na direção positiva ( + y ) .

∑ M 0 y = 0       →         M y + 50 2   mm ⋅ 500   N - 50 2   mm ⋅ 250   N = 0

M y = - 6,250   Nm

Atenção! Os dois momentos deram negativos, o que significa que a direção correta deles para o equilíbro é o oposto do que assumimos!

O momento M x aponta na verdade para - x . Ele vai causar compressão nos pontos A e B !

O momento M y aponta na verdade para - y . Ele vai causar tração em A e compressão em B !

Show, temos todos os esforços internos. Agora, com atenção para as direções, podemos calcular as tensões geradas em cada ponto e somar tudo!

Passo 3

Vamos precisar da fórmula para tensão axial:

σ = F A

Também vamos ter que usar a fórmula da flexão para cada eixo. Fique atento ao sinal! Monte a fórmula segundo os eixos que você decidiu usar!

Para o momento no eixo x : um momento positivo, na porção positiva ( y > 0 ), causa tensão na direção positiva ( z ) .

σ = M   y I x

Para o momento no eixo y : um momento positivo, na porção positiva ( x > 0 ), causa tensão na direção negativa ( - z ) .

σ = - M   x I y

Pelas fórmulas, vamos precisar da área A e do segundo momento de área.

A = 50 ⋅ 75 = 3750   mm 2

I x = 1 12 50 ⋅ 70 3 = 1757812,50   mm 4

I y = 1 12 50 3 ⋅ 70 = 781250   mm 4

Só falta fazer conta!

Passo 4

A força normal N vai causar a mesma compressão ( + z ) em ambos os pontos:

σ N = N A = 0,2   MPa

No ponto A , o momento M x comprime e o momento M y traciona

σ A = σ N + M x   y A I x - M y   x A I x

σ A = 0,2   MPa + - 9,375   Nm ⋅ ( - 75 2 mm ) 1757812,50   mm 4 - - 6,250     Nm ⋅ ( - 50 2 mm ) 781250   mm 4

σ A = 0,2   MPa

A tensão em A é de compressão!

No ponto B , o momento M x comprime e o momento M y comprime

σ B = σ N + M x   y A I x - M y   x A I x

σ B = 0,2   MPa + - 9,375   Nm ⋅ ( - 75 2 mm ) 1757812,50   mm 4 - - 6,250     Nm ⋅ 50 2 mm 781250   mm 4

σ B = 0,6   MPa

A tensão em B é de compressão!

Resposta

A tensão normal em A é de compressão:

σ A = 0,2   MPa

A tensão normal em B é de compressão:

σ A = 0,6   MPa

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro de peso desprezível repousa sobre um piso liso. Determine a distância excêntrica e y na qual a carga pode ser posicionada de modo que a tensão normal no ponto A seja nula.
Resolva o Problema 8.26 para o ponto B .
Visto que o concreto só pode suportar pouca ou nenhuma tração, esse problema pode ser evitado se o concreto for protendido com cabos ou hastes. Considere a viga simplesmente apoiada mostrada na figura
A pilastra de alvenaria está sujeita à carga de 800kN . Determine a equação da reta y=f ( x ) ao longo da qual a carga pode ser posicionada sem provocar tensão de tração na pilastra. Despreze o peso d