Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 63

O tubo estrutural mostrado na figura tem uma parede de espessura uniforme de 7,62mm. Sabendo que a força de 66,7kN é aplicada 3,8mm acima da base do tubo, determine a tensão de cisalhamento ( a ) no ponto a e ( b ) no ponto b .

Passo 1

Calcule forças e duplas na seção contendo pontos a   e b .para começarmos esse exercício gurizada :D

V x = 15 k i p s

M z = 2 - 0,15 15 = 27,75 k i p ∙ i n .

M y = 10 15 = 150 k i p ∙ i n .

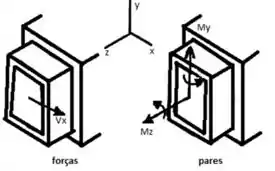
Passo 2

Tensão de cisalhamento por torque T = M z :

A = 3 - 2 0,15 4 - 2 0,15 = 9,99 i n 2

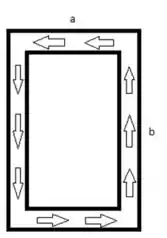
q = M z 2 A = 27,75 2 ( 9,99 ) = 1,3889 k i p /in.

Passo 3

No ponto a, t = 0,3 i n .         τ a = q t = 1,3889 0,3 = 4,630 k s i ⟵

No ponto b, t = 0,3                 τ b = q t = 1,3889 0,3 = 4,630 k s i ↑

Tensão de cisalhamento por V x :

No ponto a,

Q = Σ A x _ = 2,052 i n 3

t = 2 0,3 = 0,6 i n .

I y = 1 12 4 3 3 - 1 12 3,4 2,4 3 = 5,0832

τ = V x Q I y t = 15 2,052 5,0832 0,6 = 10,092 k s i

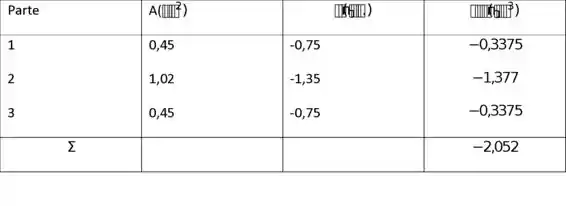
Passo 4

No ponto b, τ b = 0

Tensão de cisalhamento combinado

  1. No ponto a, τ a = 4,630 ← + 10,092 → = 5,46 k s i                     τ a = 5,46 k s i
  2. No ponto b, τ b = 4,630 ↑ + 0 = 4,63 k s i ↑                                               τ b = 4,63 k s i

Resposta

  1. τ a = 5,46 k s i
  2. τ b = 4,63 k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo de extremidade aberta tem parede de espessura 2 mm e diâmetro interno de 40 mm. Calcule a pressão que o gelo exerceu na parede interna do tubo para provocar a ruptura mostrada na figura. A tens
Sabendo que o tubo estrutural mostrado tem parede de espessura constante de 6,35 mm, determine as tensões normal e de cisalhamento nos três pontos indicados.
Sabendo que o tubo estrutural mostrado tem parede de espessura constante de 6,35 mm, determine as tensões normal e de cisalhamento nos três pontos indicados.
Para o poste e o carregamento mostrados na figura, determine as tensões principais, os planos principais e a tensão de cisalhamento máxima no ponto H.