Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 23

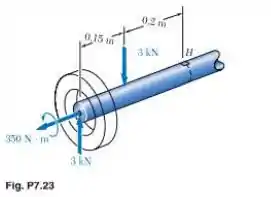
O eixo de um automóvel está sob a ação das forças e torque mostrados na figura. Sabendo que o diâmetro do eixo de seção transversal cheia é de 32 m m , determine (a) os planos e tensões principais no ponto H   localizado na superfície superior do eixo e (b) a tensão de cisalhamento máxima no mesmo ponto.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Partiu mais uma questão!

O primeiro passo para esta questão é determinar as tensões normal e de cisalhamento. Sabemos que a tensão de cisalhamento é:

τ = T c J

Onde T   é o momento torsor, c   é a distância da linha neutra e J   é o momento polar de inércia.

Portanto, teremos que:

τ = T c J = 2 T π c 3 = 2 × 350 π 16 × 10 - 3

τ = 54,399   M P a    

Já a tensão normal, é dada por:

σ = - M y I

Onde M   é o momento fletor, y   é a distância da linha neutra e I   é o momento de inércia. Logo, substituindo:

I = π c 4 4 = π 4 16 × 10 - 3 = 51,472 × 10 - 9   m 4

M = 0,15 × 3 × 1000 = 450   N m

Portanto:

σ = - 450 × 16 × 10 - 3 51,472 × 10 - 9

σ = - 139,882   M P a

Passo 2

Agora, temos o seguinte:

σ x = - 139,882   M P a

σ y = 0

τ x y = - 54,399   M P a

Portanto, vamos usar esses dados para calcularmos o raio do círculo de Mohr:

R = σ x - σ y 2 2 + τ x y 2

Substituindo:

R = 88,606   M P a

Agora, vamos calcular as tensões máxima e mínima. Para isso, temos que achar o centro do círculo, ele será dado pela tensão média:

σ m é d = 1 2 σ x + σ y = - 69,941   M P a

Ou seja, as tensões máxima e mínima serão:

σ m á x = σ m é d + R

σ m í n = σ m é d - R

Logo:

σ m á x = 18,67   M P a

σ m í n = - 158,5   M P a

Passo 3

O próximo passo é determinar a orientação dos planos principais. Sabemos que:

tan ⁡ 2 θ p = 2 τ x y σ x - σ y

2 θ p = 37,88 º

Logo:

θ = 18,9 °   e   108,9 °

Note que os dois ângulos representam a mesma orientação.

Passo 4

Por fim, sabemos que a tensão máxima cisalhante será igual ao raio do nosso círculo e, portanto:

τ m á x = R = 88,6   M P a

Resposta

  1. σ m á x = 18,67   M P a ;   σ m í n = - 158,5   M P a ;   θ = 18,9 °   e   108,9 °    
  2. τ m á x = 88,6   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque do compressor de ar está sujeito a uma pressão interna de 0,63 MPa. Se o diâmetro interno do tanque for 550 mm e a espessura da parede for 6 mm, determine as componentes da tensão que age no
Uma caldeira é feita de chapas de aço de 8 mm de espessura ligadas nas extremidades por uma junta de topo que consiste em duas chapas de cobertura de 8 mm e rebites com diâmetro de 10 mm e espaçados d
O anel cujas dimensões são mostradas na figura é colocado sobre uma membrana flexível bombeada com uma pressão p. Determine a mudança no raio interno do anel após a aplicação dessa pressão. O módulo d
O tubo de extremidade aberta feito de cloreto de polivinil tem diâmetro interno de 100 mm e espessura de 5 mm e transportar água corrente à pressão de 0,42 MPa. Se esse fluxo no interior do tubo for i
O barril está cheio de água até em cima. Determine a distância s entre o aro superior e o aro inferior de modo que a força de tração em cada aro seja a mesma. Determine também a força em cada aro. O b