Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 124

A haste uniforme ABD de 4 kg está presa à manivela BC e é ajustada com uma pequena roda que pode rolar sem atrito ao longo de uma fenda vertical. Sabendo que no instante mostrado a manivela BC gira com uma velocidade angular de 6   r a d / s   no sentido horário e uma aceleração angular de 15   r a d / s 2 no sentido anti-horário, determine a reação em A.

Passo 1

Falaaa ai galerinhaaaaa, tudo bem??

Boraaa

Desenharemos o digrama de aceleração da manivela BC.

Passo 2

Calcularemos o ponto de aceleração tangencial B usando a seguinte expressão:

α b t = B C α

Aqui α está a aceleração angular da manivela BC.

α b t = ( 0.1 ) ( 15   r a d / s 2 )

α b t = 1.5   m / s 2   ↓

Calcule o ponto de aceleração normal B usando a seguinte expressão:

α b n = B C ω 2

Aqui α está a aceleração angular da manivela BC.

Vamos substituir 0.1 m por BC e 6   r a d / s por ω .

α b n = ( 0.1   m ) ( 6   r a d / s 2 )

α b n = 3.6   m / s 2

Passo 3

Iremos desenhar o diagrama de aceleração da haste ABD.

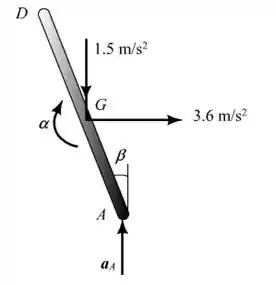
Passo 4

Iremos agora calcular o ângulo β .

β = s e n - 1 B C A B

β = s e n - 1 0.1   m 0.2   m

β = 30 °

Vamos escrever agora a relação de aceleração em A.

a A = a G + a A / G

a A = a G + - α k × r A / G

Onde a G é a aceleração da haste de cerca de L e a A / G é a aceleração relativa de um em relação ao G.

Substituindo a A J por a A , ( 3.6   i   -   1.5   j ) m / s 2 por a G e ( - 0.2   s e n   30 °   i + 0.2 cos ⁡ 30 °   j )   m por r A / G .

a A j = 3.6   i - 1.5 j + ( - α k ) ( - 0.2   s e n   30 °   i + 0.2 cos ⁡ 30 °   j )

a A j = 3.6   i - 1.5 j + ( 0.1   α   j + 0.1732   α   i   )

a A j = 0.1732 α + 3.6 i + - 1.5 + 0.1   α j

Comparando os coeficientes i

0.1732   α + 3.6 = 0

α = - 20.78   r a d / s 2

α = 20.78   r a d / s 2 (   s e n t i d o   h o r á r i o   )

Passo 5

Vamos agora desenhar o diagrama cinético.

Vamos considerar a equação momento sobre G.

∑ M G = ∑ M G e f f

A 0.1732   m =   I ¯ α

A 0.1732   m = 1 12 m L 2 α

Onde a massa m é a massa da barra e L é o comprimento da barra .

Passo 6

Substitua 4 kg por m, 0.4 m por L 20.78   r a d / s 2       p o r   α .

A 0.1732   m = 1 12 4 0.4 2 20.78

A 0.1732   m = 1.108267

A = 1.108267 0.1732

A = 6.4 0   N

Resposta

Portanto, a reação em A é 6.40   N     ← .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras AB e DE estão conectadas como mostra a figura. Sabendo que o ponto D desloca-se para a esquerda a uma velocidade de 1m / s , determine, no instante mostrado, (a) a velocidade angular de ca
Duas barras AB e DE estão conectadas como mostra a figura. Sabendo que o ponto B desloca-se para baixo com uma velocidade de 1,5m / s , determine, no instante mostrado, (a) a velocidade angular de cad
Descreva o centrodo espacial e o centrodo corporal da barra ABD do Problema 15.84. (Dica: o centrodo corporal não precisa estar sobre uma parte física da barra.)