Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 98

Duas barras AB e DE estão conectadas como mostra a figura. Sabendo que o ponto B desloca-se para baixo com uma velocidade de 1,5   m / s , determine, no instante mostrado, (a) a velocidade angular de cada barra e (b) a velocidade do ponto E.

Passo 1

Bora pra questão 98 agora, meus caros (as)!

E já sabe, né! Nada melhor do que uma figura pra ajudar a entender uma questão.

Vamos fazer um esboço destacando vetorialmente as velocidades e o centro de rotação instantâneo desse sistema, ou centros né (vai que tem mais de um).

Aqui está, nossa bela imagem...

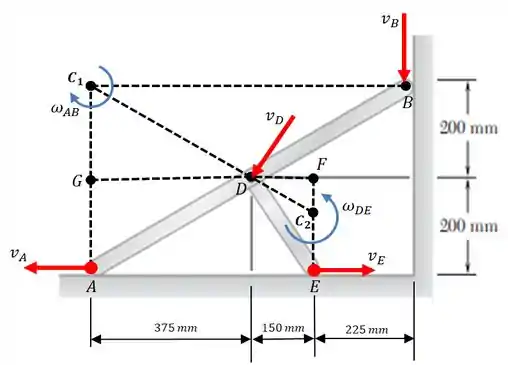
Passo 2

a) Bom! Inicialmente, a gente tem que determinar a velocidade angular de cada barra!

No esboço que fizemos anteriormente, podemos ver que o nosso sistema vai ter dois centros de rotação, que chamamos de C 1 e C 2 . Logo, vão ter duas velocidades angulares agindo aí!

A questão nos deu a velocidade com que o ponto B , está se movendo, dada por...

v B = 1,5   m / s   ↓

Só que essa velocidade v B , segundo a figura que esboçamos, vai ser dada por...

v B = B C 1 ω A B

Passo 3

De acordo com a figura do P a s s o   1 , B C 1 é dado por...

B C 1 = 750   m m

Assim, isolando ω A B :

ω A B = v B B C 1

ω A B = 1,5   m / s 0,75   m

ω A B = 2,0   r a d / s   ⤾

Obtido ω A B , podemos descobrir a velocidade em D , v D , que será dada por...

v D = D C 1 ω A B

E D C 1 , dá pra obter de boas pelo teorema de Pitágoras...

D C 1 = 200   m m 2 + 375   m m 2

D C 1 = 425   m m

Desse modo, v D será igual à...

v D = D C 1 ω A B

v D = 425   m m ( 2,0   r a d / s )

v D = 850   m m / s

Passo 4

E é com esse v D   aí que a gente obteve que seremos capazes de determinar ω D E !

Analisando a barra D E , temos que...

v D = D C 2 ω D E

E D C 2 dá pra obter de boas por semelhança de triângulos...

D C 2 D F = D C 1 D G

D C 2 = D F ⋅ D C 1 D G

D C 2 = ( 150   m m ) ⋅ 425   m m 375   m m

D C 2 = 170   m m

Logo, isolando ω D E ...

ω D E = v B D C 2

ω D E = 850   m m / s   170   m m

ω D E = 5   r a d / s   ⤿

Obtemos a velocidade angular da barra D E !

Passo 5

b) Pra finalizar, falta obter a velocidade em E , v E !

Pela figura do P a s s o   1 , temos que...

v E = E C 2 ω D E

E pra achar E C 2 , de novo vamos usar semelhança de triângulos. Temos que...

D G D F = G C 1 C 2 F

Só que...

C 2 F = 200 - E C 2

Logo;

D G D F = G C 1 C 2 F

D G D F = G C 1 200 - E C 2

375   m m 150   m m = 200   m m 200 - E C 2

2,5 = 200 200 - E C 2

500 - 2,5 E C 2 = 200

E C 2 = 700 2,5   m m

E C 2 = 280   m m

Então...

v E = E C 2 ω D E

v E = 280   m m ( 5   r a d / s )

v E = 1400   m m / s   →

Pronto! Terminamos aqui!

Bora pra frente, que atrás vem gente!

Resposta

a)

ω A B = 2,0   r a d / s   ⤾

ω D E = 5   r a d / s   ⤿

b)

v E = 1400   m m / s   →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das barras AB e BC de 3 kg tem comprimento L = 500 mm. Uma força horizontal P de intensidade de 20 N é aplicada na barra BC como mostra a figura. Sabendo que b = L (P está aplicada em C), det
A haste AB de 2 kg e a haste BC de 3 kg estão ligadas como mostra a figura a um disco que é colocado em rotação em um plano vertical a uma velocidade angular constante de 6 rad /s no sentido horário.
Um volante de motor está rigidamente preso a um eixo de 40 mm de raio que pode rolar ao longo de trilhos paralelos como mostra a figura. Quando liberado a partir do repouso, o sistema rola 5 m em 40 s
Um tambor de 100 mm de raio está preso a um disco de 200 mm de raio. O disco e o tambor têm peso combinado de 50 N e um raio de giração combinado de 150 mm. Uma corda é presa como mostra a figura e pu
Um disco uniforme de massa m = 4 kg e raio r = 150 mm é suportado por uma correia ABCD que é aparafusada no disco em B e C. Se a correia se rompe de repente em um ponto localizado entre A e B, determi