Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 15

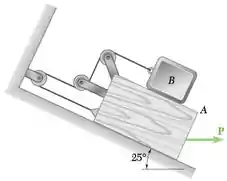
O bloco A tem a massa de 40 kg e o bloco B tem a massa de 8 kg. Os coeficientes de atrito entre todas as superfícies de contato são μ s = 0,20 e μ k = 0,15. Se P = 0, determine (a) a aceleração do bloco B e (b) a tração na corda.

Passo 1

E ai galera tudo certo? O enunciado pede que a gente determine a aceleração do bloco B e (b) a tração na corda.

Consideramos que:

2 x A + x B / A = constante

2 v A + v B / A = 0

2 a A + a B / A = 0

Agora

a B = a A + a B / A

Então

a B = a A + - 2 a A

a B = - a A

Passo 2

Primeiro, determinamos se os blocos se moverão para o valor dado de θ . Assim, buscamos o valor de θ para o qual os blocos estão em movimento iminente, com o movimento iminente de A descendo a inclinação.

B:

+ ↗ Σ F y = 0 :                 N A B - W B cos ⁡ θ = 0

N A B = m B g cos ⁡ θ

Agora

F A B = μ s N A B = 0.2 m B g cos ⁡ θ

+ ↘ Σ F x = 0 :             - T + F A B + W B sin ⁡ θ = 0

T = m B g 0.2 cos ⁡ θ + sin ⁡ θ

Passo 3

A:

+ ↗ Σ F y = 0 :               N A - N A B - W A cos ⁡ θ = 0

ou

N A = m A + m B g cos ⁡ θ

Agora

F A = μ s N A = 0.2 m A + m B g cos ⁡ θ

+ ↘ Σ F x = 0 :             - T - F A - F A B + W A sin ⁡ θ = 0

Passo 4

T = m A g sin ⁡ θ - 0.2 m A + m B g cos ⁡ θ - 0.2 m B g cos ⁡ θ

= g m A sin ⁡ θ - 0.2 m A + 2 m B cos ⁡ θ

= g m A sin ⁡ θ - 0.2 m A + 2 m B cos ⁡ θ

Equacionando as duas expressões para T

m B g 0.2 cos ⁡ θ + sin ⁡ θ = g m A sin ⁡ θ - 0.2 m A + 2 m B cos ⁡ θ

8 0.2 + tan ⁡ θ = 40 tan ⁡ θ - 0.2 40 + 2 × 8

tan ⁡ θ = 0.4

ou θ = 21.8 ° para movimento iminente. Desde θ ° , os blocos se moverão. Agora considere o movimento dos blocos.

Passo 5

  1. + ↗ Σ F y = 0 :               N A B - W B cos ⁡ 25 ° = 0

    ou

    N A B = m B g cos ⁡ 25 °

    Deslizante:

    F A B = μ k N A B = 0.15 m B g cos ⁡ 25 °

    + ↘ Σ F x = m B a B :             - T + F A B + W B sin ⁡ 25 ° = m B a B

    ou

    T = m B g 0.15 cos ⁡ 25 ° + sin ⁡ 25 ° - a B = 8 9.81 0.15 cos ⁡ 25 ° + sin ⁡ 25 ° - a B

    = 8 5.47952 - a B               N

    + ↗ Σ F y = 0 :               N A B - N A B - W B cos ⁡ 25 ° = 0

    Passo 6

    N A = m A + m B g cos ⁡ 25 °

    Deslizante:

    F A = μ k N A = 0.15 m A + m B g cos ⁡ 25 °

    + ↘ Σ F x = m A a A :             - T - F A - F A B + W A sin ⁡ 25 ° = m A a A

    Substituindo e usando Eq. (1)

    T = m A g sin ⁡ 25 ° - 0.15 m A + m B g cos ⁡ 25 °

    - 0.15 m B g cos ⁡ 25 ° - m A - A B

    = g m A sin ⁡ 25 ° - 0.15 m A + 2 m B cos ⁡ 25 ° + m A a B

    = 9.81 40 sin ⁡ 25 ° - 0.15 40 + 2 × 28 cos ⁡ 25 ° + 40 a B

    = 91.15202 + 40 a B               N

    Equacionando as duas expressões para T

    8 5.14952 - a B = 91.15202 + 40 a B

    ou

    a B = - 0.98575   m/ s 2

    Passo 7

  2. Nós temos

T = 8 5.47952 - - 0.98575

Resposta

a )   a B = 0.986   m/ s 2     25 °

b )   T = 51.7   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para descarregar uma pilha de madeira compensada de um caminhão, o motorista primeiro inclina a carroceria do caminhão e depois acelera do repouso. Saber que os coeficientes de atrito entre a folha de
O bloco A tem uma massa de 40 kg e o bloco B tem uma massa de 8 kg. Os coeficientes de atrito entre todas as superfícies de contato são μ s = 0,20 e μ k = 0,15. Se P = 40 N -, determine (a) a aceleraç
Um satélite artificial de 200 kg está em órbita circular de 1.500 km sobre a superfície de Vênus. A aceleração devido à atração gravitacional em Vênus nesta altitude é 5,52 m/s2. Determine a intensida
Determine a velocidade máxima teórica que um automóvel de 2.700 lb partindo do repouso pode atingir após viajar um quarto de milha se a resistência do ar for considerada. Suponha que o coeficiente de
Cada um dos sistemas mostrados está inicialmente em repouso. Negligenciando o atrito do eixo e as massas das polias, determine para cada sistema (a) a aceleração do bloco A, (b) a velocidade do bloco