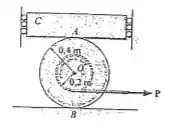
O bloco tem uma massa de e está confinado entre duas paredes por roletes lisos. Se o bloco se apoia no topo do carretel de determine a força mínima do cabo necessária para mover o carretel. O cabo está enrolado no núcleo do carretel. Os coeficientes de atrito estático em e são e .

Queremos encontrar o valor mínimo para a força que é necessária para que o carretel se mova. Sendo assim, tomemos o seguinte diagrama de forças

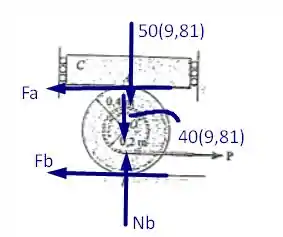
Utilizando as equações de equilíbrio teremos

Se assumirmos, aqui, um deslizamento em vamos ter

Agora, conseguimos resolver as equações do equilíbrio e vamos encontrar

Olhando para o valor máximo de vamos ter

Temos que nosso valor de encontrado como consequência da nossa hipótese inicial é, de fato, o valor mínimo de .