Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 24
Determine a intensidade do momento de binário necessário para suportar o cilindro de na configuração mostrada. A ranhura lisa em pode deslizar livremente dentro da ranhura. Despreze a massa dos membros.
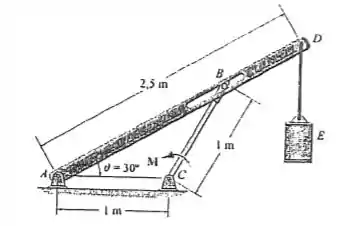
Passo 1
Desejamos determinar o valor de , para isso façamos a seguinte construção auxiliar em na nossa figura original.
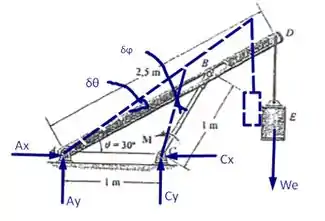
Passo 2
A posição do ponto de aplicação de é especificado pela posição de coordenada , medido a partir do ponto fixo . Assim, temos
Além disso, da geometria do problema podemos inferir que
Das equações de trabalho virtual, vamos encontrar que
Lembrando que e substituindo as equações na equação acima vamos obter
Tendo em mente que vamos obter
Resposta
Exercícios de Livros Relacionados
A força horizontal de 20N atua sobre o cabo da chave de soquete. Determine o momento dessa força em relação ao ponto O. Especifique os ângulos diretores coordenados α ,β ,γ do eixo do momento.
O cabo de reboque exerce uma força P = 6k N na extremidade da lança do guindaste de 8m de comprimento. Se x = 10m , determine a posição θ da lança para que essa força crie um momento máximo em relação
A grua pode ser ajustada para qualquer ângulo 0 ° ≤ θ ≤ 90 ° e qualquer extensão 0 ≤ x ≤ 5m . Para uma massa suspensa de 120k g , determine o momento desenvolvido em A em função de x e θ . Que valores
O virabrequim está sujeito a um torque M = 50N · m . Determine a força compressiva horizontal F aplicada ao pistão para o equilíbrio quando θ = 60 ° .
A lixeira tem peso W e centro de gravidade em G . Determine a força no cilindro hidráulico necessária para mantê-la na posição genérica θ .