Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 216
Determine a equação de restrição que relaciona as acelerações dos corpos e . Assuma que a superfície superior de permanece na horizontal.
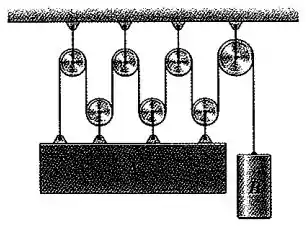
Passo 1
Considere como a distância vertical entre os centros de uma polia móvel e de uma polia fixa no teto, e como a distância vertical entre o bloco e a polia fixa no teto acima de . Temos que o comprimento total da corda é:
Portanto, se derivarmos em relação ao tempo, obteremos:
Derivando mais uma vez:
Portanto, a equação de restrição que relaciona as acelerações é:
Resposta
Exercícios de Livros Relacionados
2/120) Para um dado valor de y , determine a velocidade ascendente de A em termos da velocidade descendente de B . Despreze os diâmetros das polias .
2/11( Determine a relação que regula as velocidades dos quatro cilindros. Expresse todas as velocidade para baixo como positivas . Quantos graus de liberdade existem?
2/118) Para o sistema de polias mostrado , cada um dos cabos em A e B recebe uma velocidade de 2 m / s na direção da seta . Determine a velocidade ascendente v da carga m .
Um caminhão equipado com um guincho motorizado sobre a sua dianteira puxa a si próprio para cima num aclive íngreme com o arranjo de cabo e polia mostrado. Se o cabo é enrolado sobre o tambor na taxa
Em um dado instante, o cilindro A tem uma velocidade para baixo de 0,8m / s e uma aceleração para cima de 2m / s 2 . Determine a velocidade e a aceleração correspondentes do cilindro B .