Uma placa plana uniforme de massa na forma de um quadrante circular de raio está fixada ao aro de massa desprezível na posição indicada. Se o aro e o quadrante são liberados a partir do repouso nessa posição sobre uma superfície horizontal e rolam sem deslizar, determine a força de atrito inicial .
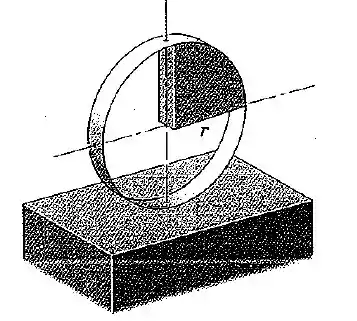
Passo 1
Vamos começar encontrando o momento de inércia do sistema em relação ao centro de massa.
Como o aro tem massa desprezível, o centro de massa do sistema é simplesmente o centro de massa do quadrante circular:
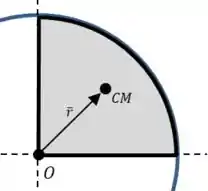
Então vamos usar o teorema dos eixos paralelos:
O momento é tabelado, e queremos descobrir :
E também é tabelado:
Passo 2
Agora vamos montar equações que nos deem as forças que agem sobre o aro. Mas primeiro precisamos de um diagrama:
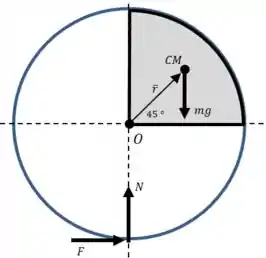
Começamos com uma equação para os momentos em relação ao centro de massa:
E as forças que produzem momento em relação a esse ponto são , e :
E lembrando que :
Essa é nossa primeira equação.
Passo 3
Agora vamos usar a segunda lei de Newton para determinar novas equações:
A única força que age nessa direção é a força de atrito :
E a componente da aceleração nessa direção?
Temos a aceleração associada ao movimento de translação do centro de massa do sistema, somada à componente aceleração angular associado à rotação do centro de massa em torno do ponto .
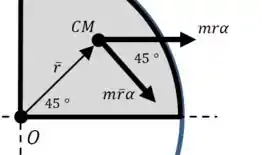
E então:
Passo 4
E precisamos fazer a mesma coisa para a direção vertical:
E as forças que agem nessa direção são e :
E a aceleração do centro de massa só tem a seguinte componente nessa direção (dê uma olhada no desenho do passo anterior):
Então:
Passo 5
Agora ficamos com um sistema de três equações:
E nosso objetivo é resolver esses sistema para encontrar . Vamos simplificar algumas coisas:
Substituindo a primeira e a segunda na terceira:
Vamos dividir tudo por :
E agora vamos “abrir” todos esses parênteses:
E já podemos somar alguns termos:
Agora podemos substituir isso na segunda equação do sistema para encontrar :
Resposta
A força de atrito inicial é .