Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 35

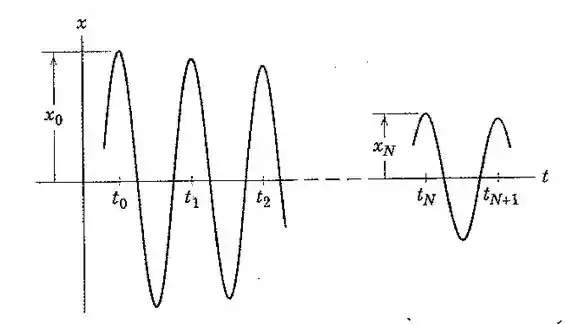
35. A figura representa a relação deslocamento-tempo medida para uma vibração com um amortecimento pequeno, onde é impraticável se alcançar resultados precisos medindo as amplitudes aproximadamente iguais de dois ciclos sucessivos. Modifique a expressão para o fator de amortecimento viscoso 𝜉 baseado na medida das amplitudes x 0 e x N , que estão separadas de N ciclos.

Passo 1

Bom! A razão entre duas amplitudes x 0 e x N , separadas de N ciclos, é dada pela seguinte relação abaixo:

x 0 x N = C e - ξ ω n t 0 C e - ξ ω n ( t 0 + N τ d )

x 0 x N = e - ξ ω n t 0 e - ξ ω n ( t 0 + N τ d )

x 0 x N = e - ξ ω n t 0 + ξ ω n ( t 0 + N τ d )

x 0 x N = e ξ ω n N τ d

E também não podemos esquecer do decremento logarítmico δ n , cuja fórmula em razão das amplitudes separadas de N ciclos, tem a seguinte aparência:

δ n = l n l n   x 0 x N  

Só que x 0 / x N , já obtivemos no P a s s o   1 . Vamos então, substituí-lo na fórmula do decremento:

δ n = l n l n   e ξ ω n N τ d  

δ n = ξ ω n N τ d

Pronto! Já encontramos algo interessante para usarmos posteriormente.

Passo 2

Obtida uma nova expressão para o decremento logarítmico δ , bora então lembrar da fórmula da frequência amortecida τ d , que tem a cara abaixo:

τ d = 2 π ω n 1 - ξ 2

Agora, o que temos que fazer é escrever esse τ d em função da última relação que obtivemos lá no final do P a s s o   1 :

δ n ξ ω n N = 2 π ω n 1 - ξ 2

δ n = ξ ω n N 2 π ω n 1 - ξ 2

δ n = ξ N 2 π 1 - ξ 2

Elevam-se os dois lados da equação acima, ao quadrado:

( δ n ) 2 = ξ N 2 π 1 - ξ 2 2

δ n 2 = ξ 2 N 2 π 2 1 - ξ 2

δ n 2 - ξ 2 δ n 2 = ξ 2 N 2 π 2

ξ 2 N 2 π 2 + ξ 2 δ n 2 = δ n 2

ξ 2 N 2 π 2 + δ n 2 = δ n 2

ξ = δ n 2 N 2 π 2 + δ n 2

ξ = δ n N 2 π 2 + δ n 2

E encontramos a nossa querida resposta.

Resposta

ξ = δ n N 2 π 2 + δ n 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32. Um oscilador harmônico linear que possui uma massa de 1,10k g é colocado em movimento com um amortecimento viscoso. Se a frequência é de 10H z e se duas amplitudes sucessivas separadas de um ciclo
No exemplo 15 - 7 , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?Exemplo 15 - 7 : m = 250g , k = 85N / m e b = 70g / s , T = 0,34s . A amplitude é d
27. Um pedaço de 3k g de massa de vidraceiro cai de uma altura de 2m sobre o bloco de 28k g inicialmente parado, que é apoiado por quatro molas, cada uma das quais possui uma constante k = 800N / m .
Um oscilador criticamente amortecido, partindo da posição de equilíbrio, recebe um impulso que lhe comunica uma velocidade inicial v 0 . Verifica-se que ele passa por seu deslocamento máximo, igual a
Seja r a razão entre dois máximos consecutivos do deslocamento de um oscilador livre fracamente amortecido ( γ ≪ ω 0 ). O parâmeto δ = ln ⁡ r chama-se decremento logarítmico. (a) Relacione δ com a con