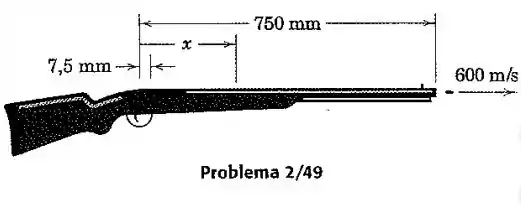
Com uma boa aproximação a pressão atrás de uma bala de espingarda varia inversamente com a posição do ponto ao longo do cano. Assim, a aceleração da bala pode ser escrita como , onde é uma constante. Se a bala parte do repouso em e se a velocidade de saída da bala é de no final dos do cano, calcule a aceleração da bala quando esta passa o ponto médio do cano em .
Passo 1
Galera, aqui queremos achar a aceleração quando , mas já sabemos que essa aceleração vai ser dada por . Então, o que precisamos fazer é calcular a constante . Mas como?
Pra isso, temos que usar uma equação diferencial em que apareça a aceleração , então temos duas opções:
Porém, como o exercício já nos deu as velocidades e as distâncias, é melhor usar a equação:
Passo 2
Então, substituindo o valor na equação, temos:
Agora a gente manda ver na integração! Lembrando de converter e :
Passo 3
Show! Agora que temos o valor de , basta substituir na expressão de pra achar a aceleração em :