Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 56
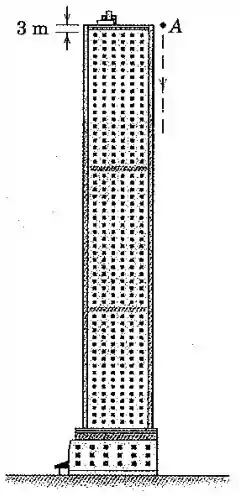
Os pavimentos de um edifício alto são uniformemente espaçados de metros de altura. Uma bola é deixada cair da posição mostrada do telhado. Determine os tempos necessários para que esta passe os metros do primeiro, décimo e centésimo andares (contados a partir do topo). Despreze o arrasto aerodinâmico.
Passo 1
Galera, como temos a aceleração constante , a velocidade vai ser dada por
Então podemos integrar a seguinte equação diferencial:
onde é o número do andar e é o tempo gasto do topo até o fim do -ésimo andar.
Passo 2
Show! Agora vamos resolver as integrais pra isolar :
Sabendo que , podemos calcular , , , , e :
Finalmente, podemos calcular os tempos para que a bola passe apenas os metros de cada andar, sendo este tempo para o -ésimo andar:
Resposta
Exercícios de Livros Relacionados
O movimento de uma partícula e definido pelas equações x = 4t3 - 5t2 + 5t e y = 5t2 - 15t, onde x e y são expressos em milímetros e t e expresso em segundos. Determine a velocidade e a aceleração quan
O movimento tridimensional de uma partícula é definido pelo vetor de posição r = (Rt cos ω nt)i + ctj + (Rt sen ω nt)k. Determine as intensidades da velocidade e aceleração da partícula. (A curva espa
Um aeroplano usado para jogar água sobre um incêndio florestal está voando horizontalmente em linha reta a 315 km/h a uma altitude de 80 m. Determine a distância d na qual o piloto deverá liberar a ág
Para a partícula do Problema 11.63, trace a curva a-t e determine usando o método da Seção 11.8, (a) a posição da partícula quando t = 52 s, (b) o valor máximo de sua posição coordenada.
Três crianças estão jogando bolas de neve umas nas outras. A criança A joga uma bola de neve com velocidade horizontal v0. Se a bola de neve passa sobre a cabeça da criança B e atinge a criança C, det