Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 188
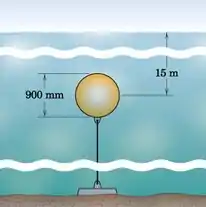
Uma bóia esférica de aço de 150 kg de 900 mm de diâmetro deve ser ancorada em água salgada 15 m abaixo da superfície. Encontre a massa m de sucata a ser vedada dentro da bóia para que a tensão no cabo da âncora onde ele se liga à bóia não ultrapasse 1,5 kN. Para mudanças desprezíveis na densidade da água, a flutuabilidade depende da profundidade de submersão?
Passo 1
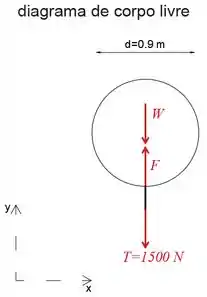
Primeiro, isolaremos e desenharemos o diagrama de corpo livre do aço esférico com o peso do aço e da sucata de ferro, a tensão do cabo e a força de flutuação atuando nele.
O peso total atuando é:
A partir daqui, podemos expressar a massa do ferro como:
Passo 2
Observe que assumiremos que a mudança na densidade da água é desprezível, portanto, a mudança na pressão da água circundante (causada pela mudança na altura) agindo para cima no aço esférico é igual à mudança na pressão da água agindo para baixo. Isso significa que a flutuabilidade não depende da profundidade
A força de empuxo é igual ao produto da densidade, volume e gravidade da água.
O volume da esfera é:
Passo 3
Substitua V e g por seus valores e por 1030 kg/m3 na expressão para F
Passo 4
Equacionando a soma das forças na direção y a zero, podemos determinar o peso total W.
Finalmente, substituiremos W por seu valor na equação (1) para determinar a massa da sucata de ferro.