Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 183
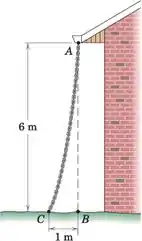
Por razões estéticas, às vezes são usadas correntes em vez de calhas em prédios pequenos, a fim de direcionar a água de escoamento do telhado da calha para o nível do solo. O arquiteto do edifício ilustrado especificou uma corrente vertical de 6 m de A a B, mas o construtor decidiu usar uma corrente de 6,1 m de A a C, conforme mostrado, a fim de colocar a água mais longe da estrutura. Em que porcentagem n o construtor aumentou a magnitude da força exercida na calha em A em relação à calculada pelo arquiteto? A corrente pesa 100 N por metro de comprimento.
Passo 1
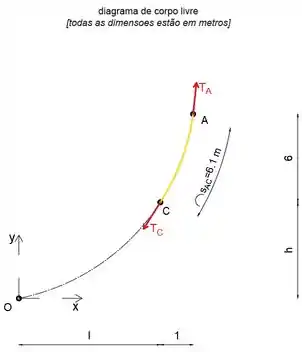
Primeiro, desenharemos o diagrama de corpo livre do cabo. Imagine que o cabo não termina em C, em vez disso, continua até chegar ao ponto mais baixo, esse ponto será marcado como o início do sistema de coordenadas.
Olhando para o esboço, podemos ver que as coordenadas dos pontos A e C são:
E o peso por unidade de comprimento é:
Passo 2
A seguir, uma vez que o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catenária, então usaremos a expressão (5/19)
Substitua m por seu valor e coloque as coordenadas dos pontos A e C na equação.
Ponto C:
Ponto A:
Observe que, subtraindo a equação (A.1) e (C.1), eliminaremos o h desconhecido.
Passo 3
Uma vez que existem duas incógnitas figurando na equação (1), precisaremos escrever outra equação onde essas duas (l e T0) são as únicas incógnitas.
Sabemos que o comprimento do cabo do ponto A ao C é:
Podemos escrever este comprimento como a diferença entre o comprimento do ponto O ao B e do ponto O ao A
Usando a expressão (5/20), podemos escrever sA e sB como:
Passo 4
Substitua sA e sB pelas expressões (A.2) e (B.2) na equação (2)
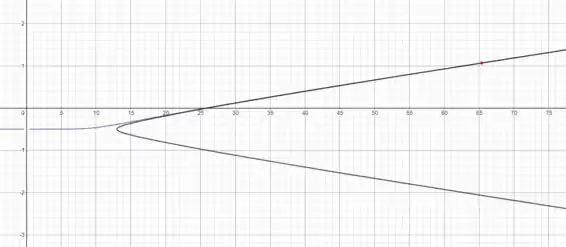
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos as equações (1) e (2.1) e leremos os valores de T0 e l que satisfazem ambas as equações.
Observe que você precisará ampliar o diagrama para poder ler os resultados.
Os resultados lidos no diagrama:
Usando a expressão (5/21), podemos determinar a tensão no ponto A
Passo 5
Substitua T0 e por seus valores e coloque as coordenadas necessárias nas expressões acima.
Finalmente, substitua l por seu valor.
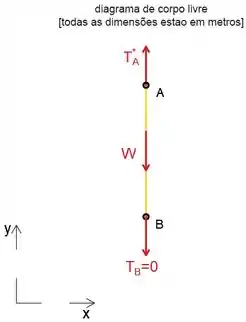
Agora vamos desenhar o diagrama de corpo livre do cabo vertical de 6 m de comprimento conectado nos pontos A e B.
Passo 6
Observe que, como a distância do cabo é exatamente igual à distância entre os pontos A e B, todo o peso é suportado pelo pino em A, enquanto a tensão em B é igual a zero.
O peso total do cabo é:
Passo 7
Ao igualar a soma das forças na direção y a zero, podemos determinar a força
Por fim, compararemos os resultados e para calcular o aumento da tensão em porcentagem.